円 面積 積分
円筒の体積=底面積(円の面積半径×半径×円周率)×高さ です 比重=密度で計算するならば、水が1gになる体積1cm3を利用するために長さの単位をcmに直して計算してください 計算結果はgで出るのでこれをkgに直してください 最初からkgで出したい時は.
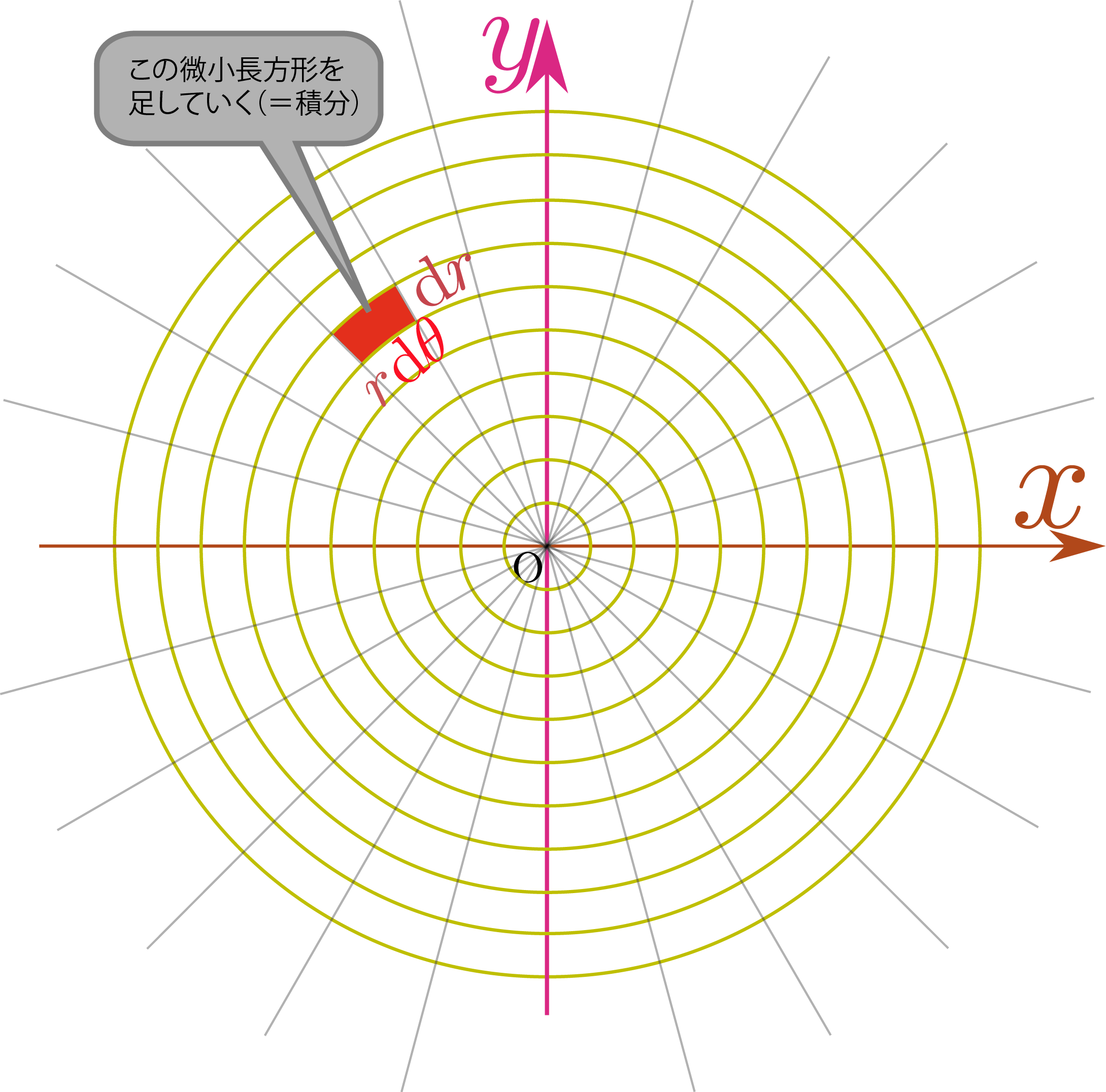
円 面積 積分. まず、面積ベクトルを図のように原点から外側を正としてとります。すると なので となります。ここで です。よって、 で、 なので が得られます。これを積分すれば , , , , が得られます。 このようにベクトル関数 と領域 に対して をベクトル関数の面積分. 面積が 113.04(cm 2)の円の半径を求めてください。ただし円周率を 3.14とします。 ただし円周率を 3.14とします。 円の面積を求める公式は. Dr^2 の積分が必要? 円の面積を求める方法の1つに、2次元極座標で \(r\) 方向と \(\theta\) 方向の格子に分割して、.
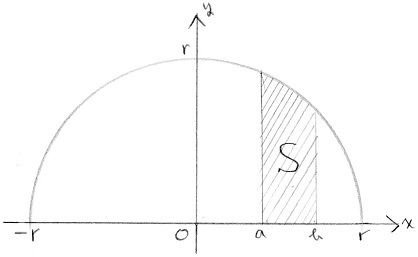
S = 1017.876 円周の長さ:. 円の面積は、S=∫-1 1 2√(1-x 2)dx で、非積分関数は連続有界なので、この定積分は有 限値であるというのは曲線の長さ等とは関係ないので循環してないと思いました。. Enjoy the videos and music you love, upload original content, and share it all with friends, family, and the world on YouTube.
円の面積の関数\( S(r) \)は微分すると円周になると言えるわけです(完璧さを求める方は\( h<0 \)の場合も考察してください。以下の球の議論でも同様)。 言い換えれば、円の面積は円周\( 2\pi r \)の積分\( \displaystyle \int 2\pi r dr =\pi r^2\)と計算できるのです。. 数学・算数 - 円S(r,2π)=πr^2を微分したら、なぜ円周の長さ2πrに等しくなるのでしょうか? たしか、微分は接線の傾きを求めるものだったと思うのですが。 よろしくお願いします。. R = 18 円の面積:.
弓形の面積(中心角から) 弓形の面積(弓形の半径と高さから) 弓形の面積(弓形の弦長と高さ. なので、 $0$ から $3$ まで積分するということは、この円の右上の部分である $\dfrac{1}{4}$ を表しているので、\ \frac{3^2}{4}\pi \となり、これを $\dfrac{8}{3}$ 倍して、楕円の面積が $6\pi$ とあることがわかります。. 円の面積を求める公式は、S = πr^2 で表されます。このページでは、円の面積の求め方を、計算問題と共に説明しています。また、公式の導き方のイメージも説明しています。.
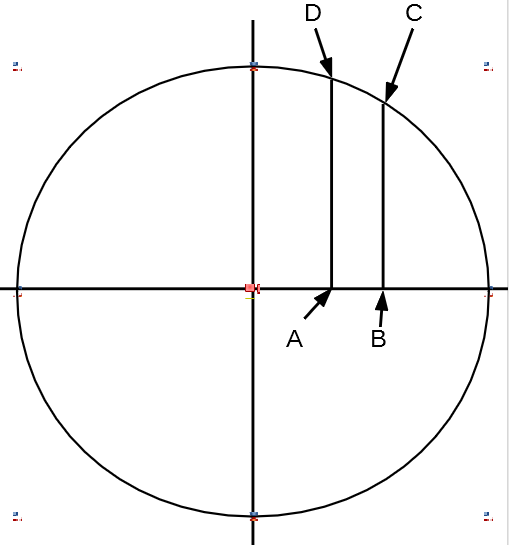
3 積分法の応用 (数学Ⅲ 積分法) 関連語句:円の面積,楕円の面積,サイクロイドの面積,置換積分,媒介変数,パラメータ. 円を直線で切った時の面積の計算方法を教えてください。 半径rの円の一番底からHの高さで直線で切った時の面積を計算する方法を教えてください。rとHだけの式でできるでしょうか? 図のように線を引き、 OABを定めるOA=r-hとなるので、三平方の定理より、AB=√(2rh-h^2)また、∠AOB=θとおくと. 弓形の面積(中心角から) 弓形の面積(弓形の半径と高さから) 弓形の面積(弓形の弦長と高さ.
大きな円の面積から小さな引いたあと,定積分して,$\sin$ 置換 → 半角の公式。 シェアする Twitter Facebook はてブ Pocket LINE コピー. 円の面積の公式から半径を計算したあと 「半径⇒直径⇒円周の長さ」の順に求めていきます。 公式に当てはめることで、円周の長さが \(43.96cm\) と求まりました。. 応用2つの円の交点を通る円や直線 views 基本相関係数と散布図の関係 views 標準二次方程式が実数解を持つ範囲 views 基本三角形の.
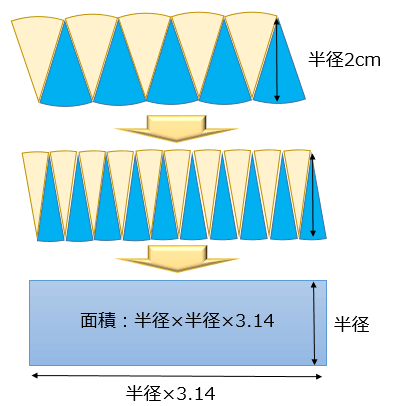
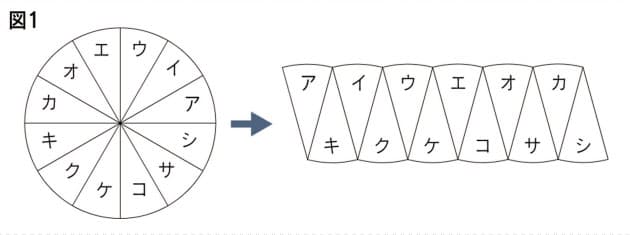
求める面積を S とすると、 上式の定積分の計算は、置換積分を用いてもいいが、軽妙に「四分円の面積」から求め る方が多数だろう。 また、この楕円は、半径 a の円を y 軸方向に b/a 倍縮小して得られるという性質を用い て、. 円周を積分 = 円の面積 球の表面積を積分 = 球の体積 逆に、 円の面積を微分 = 円周 球の体積を微分 = 球の表面積 この関係が理解できたら、 公式丸暗記からは解放されて楽になりますね! 「積分」は、. 円の面積の公式や円周率が3より少し大きな数になることの証明である。 聞かれたときにすぐ答え、大人の威厳を取り戻そう。 円を扇形に切って.
積分の発想。円周率と円の面積 円の定義 平面における円とは、そもそも中心点を囲っている閉じた線(「閉曲線(Closed curve)」)がある場合の、その閉曲線(「周長(perimeter)」)上のどの点からでも中心点との距離が一定であるような図形である。. 表面積を積分する(足し合わせる)と体積になる。 つまり、体積の微分が表面積。 \((\displaystyle\frac{4}{3}\pi r^3)’=4\pi r^2\) おまけ 円錐を積分で計算してみましょう。 底面の半径\(r\)、高さ\(h\)とする。 底面の中心を原点に、頂点に向かって軸を取る。. この立体の体積は、三角形の面積を積み上げた形として考えましょう。三角形の面積を積分すると体積になります。 ここで、三角形を PQR として面積を求めてみます。$45\text°$ で切断しているので、この三角形は底辺と高さが等しい直角二等辺三角形です。.
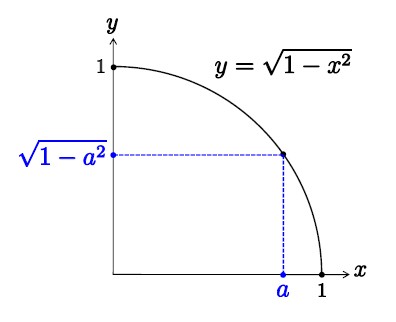
この部分の面積は近似的に です。従って、量の求め方の原理によれば半径rの円の面積sは次の式で与えられます。 これが理由なのです。第2辺をrで微分すると となるわけですね(微分積分学の基本定理)。平たく言うと「積分して微分すれば元に戻るから」。. ここで積分領域 が円なので極座標に置きたくなるが、極座標にしてしまうと の部分が計算しにくくなるので今回は極座標には変換しない。 2重積分ができる形に積分範囲を置き換え ここで、\y^2 \leqq a^2 - x^2 \である。さらに より、\0 \leqq y \leqq \sqrt{a^2 - x^2}. 面積が円のちょうど3倍 S=3·πa 2 になるのは,興味深いことです. 問題1 次の途中計算を参考にして x= sin t , y= sin 2t (0≦t≦π) で囲まれる図形の面積を求めてください.
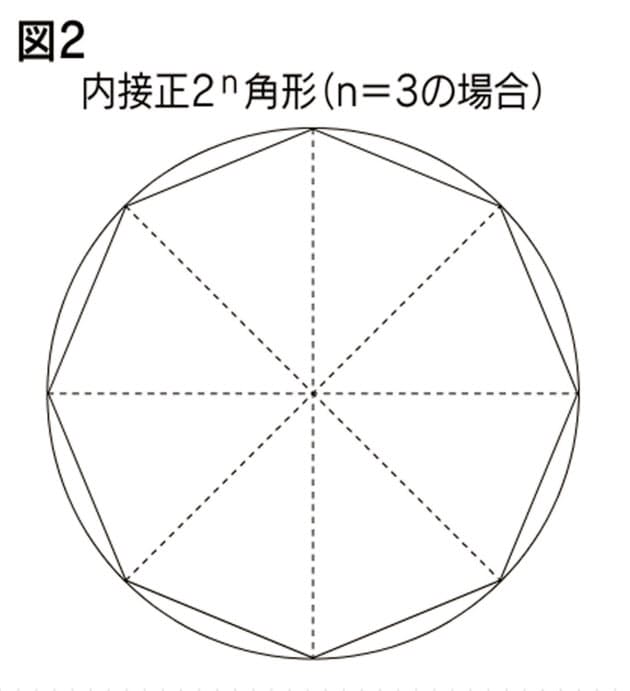
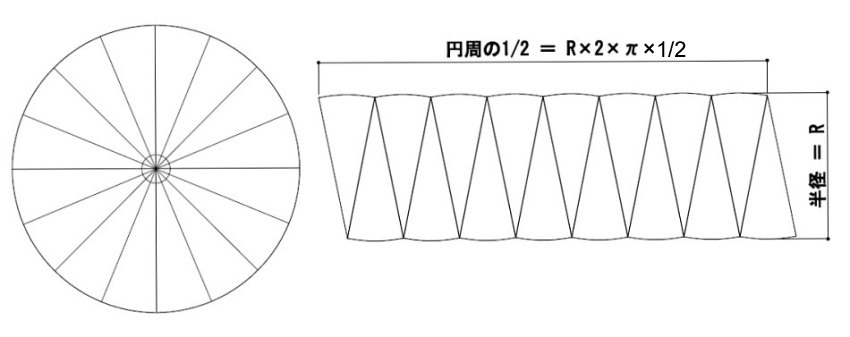
円の面積= π £(半径)2 より得られるので、その求め方を思い出しその際にlim θ!0 sinθ θ = 1 を用いてい ることを確認する。 下図のように半径r の円を上下で切り離して2n 等分した扇形を交互に はめていく。 円の面積は等分した扇形の弧を弦に代えてできる. 球の表面積は,半径,y,の円に微小な厚みをかけた円帯を足し合わせていったものですから,半球の表面積は, となります. ここで,なぜ,x軸に沿っての積分,dx,ではないか,の説明は, こちら ,のサイトに丁寧に書かれているので,参考にしてみて. L = 113.097 ここでは半径「10」、「18」の円の面積と円周の長さを計算してみました。 その他のサンプルプログラムも合わせてご覧ください。.
円の面積がなぜ \( \pi r^2 \) ( \( r \) は半径 ) になるのかを説明します。 (使っている図が悪いので後日差し替えます。) 掛け算で三角形の面積を求めるものの、その他の積分計算や極限計算は使わないようにしました。 掛け算の記号 ( \( \times \) ) を省略することと、. 円とおうぎ形⑹ - 弓形の面積 1 ステップ1 弓形(ゆみがた)の面積を求める 1 次の図は、おうぎ形と直角二等辺三角形を組み合わせた図形です。色 のついた部分の面積を求めなさい。ただし円周率は3.14とします。 ※ 図のように、おうぎ形の弧 こ.

積分法の話題3 放物線と円とで囲まれた部分の面積 高校数学 身勝手な主張
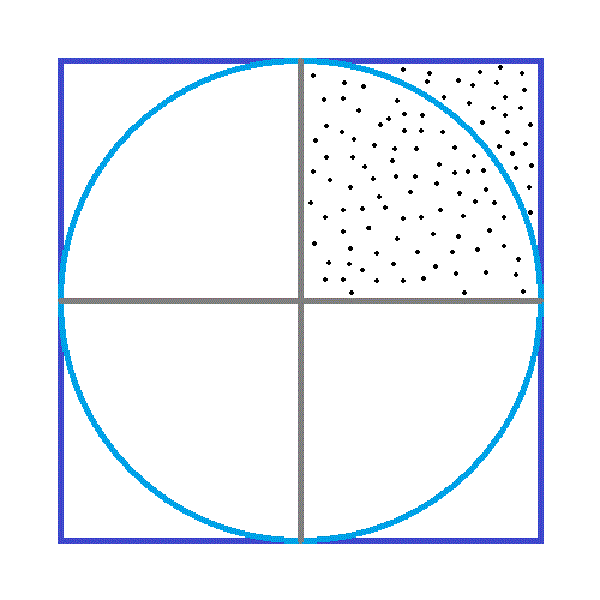
モンテカルロ法による円の面積計算
面積を求める
円 面積 積分 のギャラリー
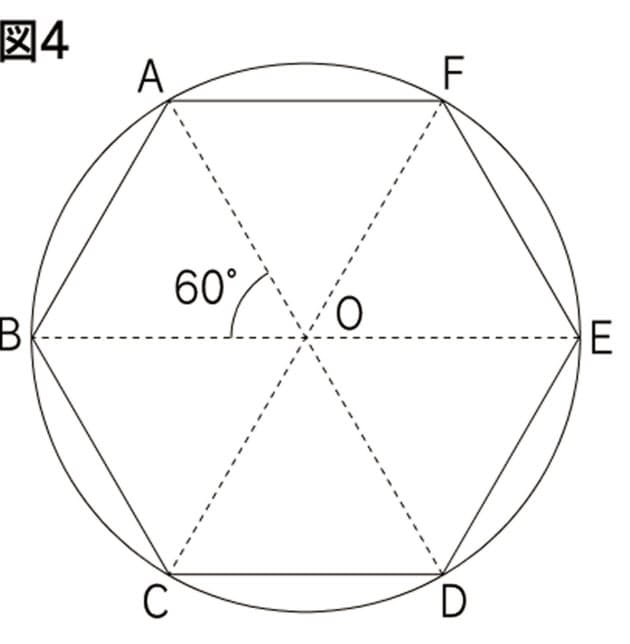
子供に説明できる 円の面積の公式 の証明 働き方 学び方 Nikkei Style
Q Tbn 3aand9gctj3goo5njmuwc 7pm2d T9knxkls8ofsc90dliywxdejwyqaiv Usqp Cau
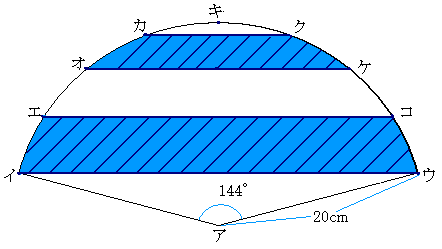
問題93おうぎ形の面積
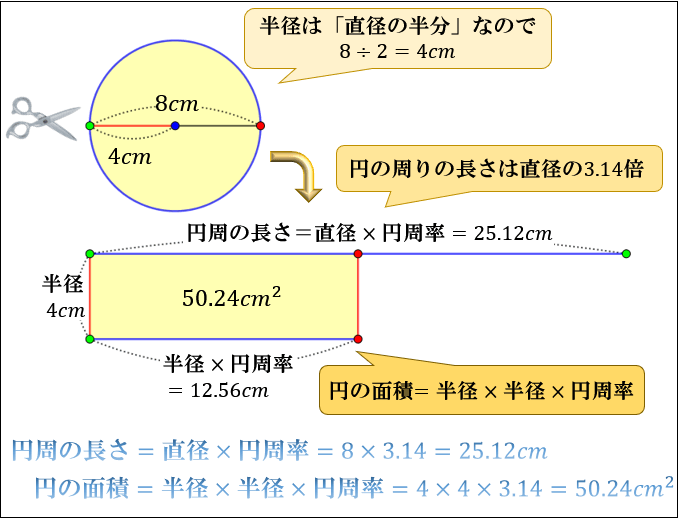
円周の求め方と円の面積について アタリマエ

高校数学 定積分と面積 2 問題編 映像授業のtry It トライイット

円積問題 Wikipedia

極座標で円の面積を求める方法の補足 Fun Fun 物理
電気磁気工学を学ぶ 積分と円の面積
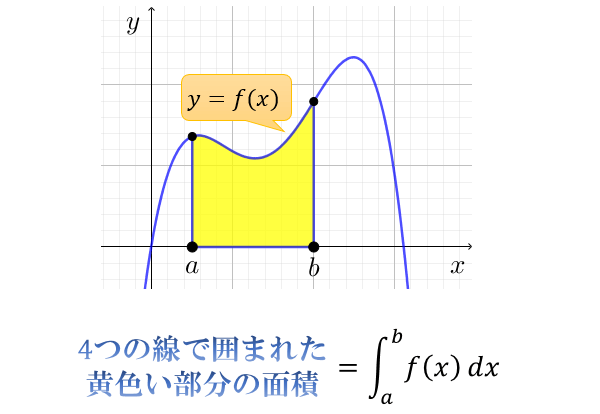
積分とは何なのか 面積と積分計算の意味 アタリマエ

積分法の話題3 放物線と円とで囲まれた部分の面積 高校数学 身勝手な主張
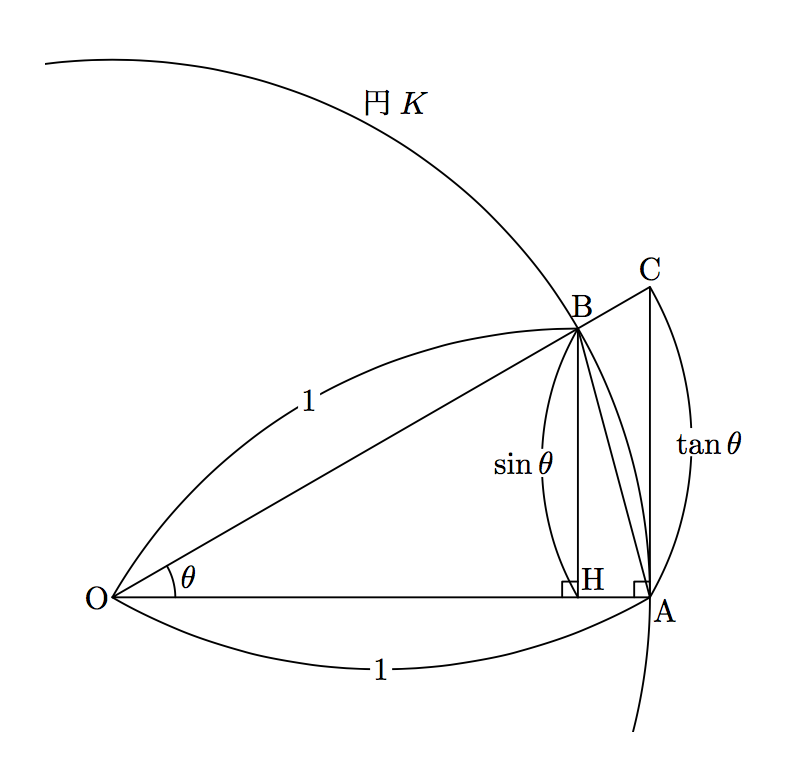
Sin8 8 1 の高校での証明は循環論法ではない Saitei Net
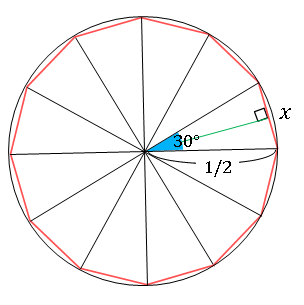
円の面積と周長
面積分
楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ

円の面積の求め方 公式と計算例
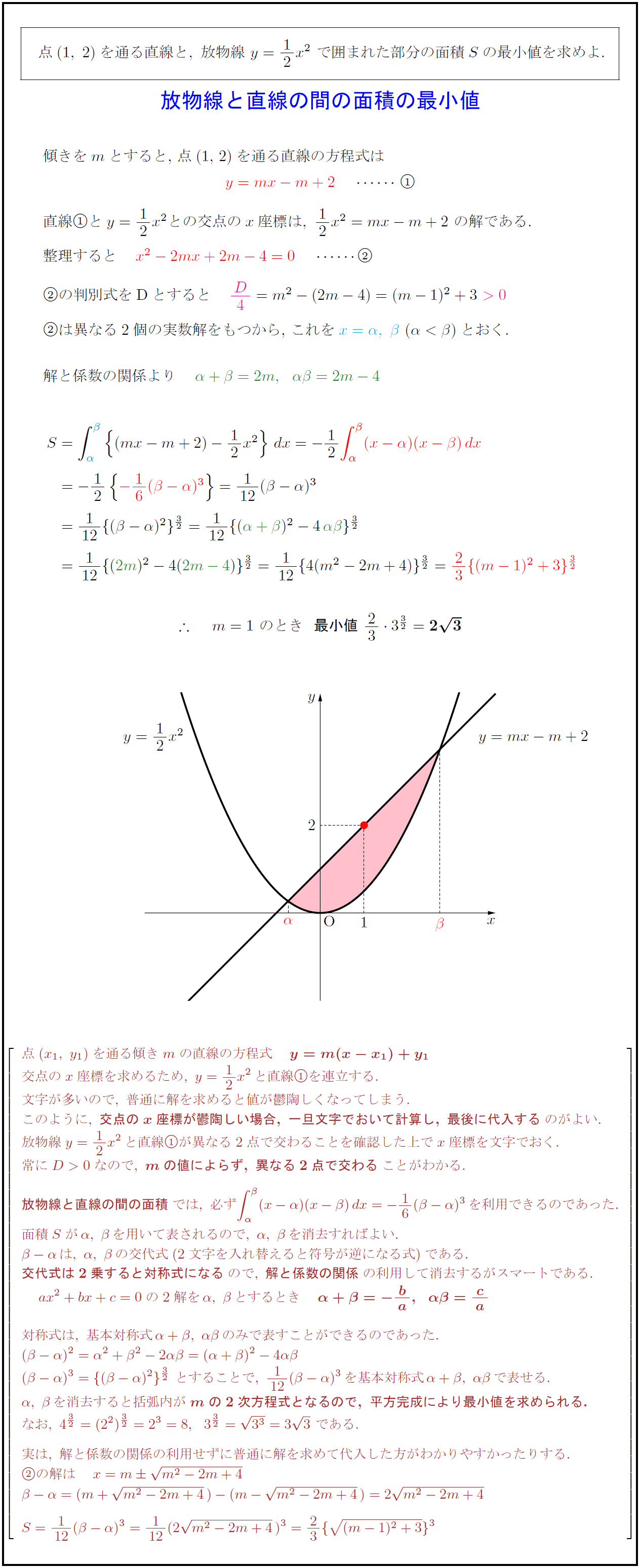
高校数学 放物線と直線の間の面積の最小値 1 6公式の利用 受験の月

数値積分による円の面積の計算 Java プログラミング 入門
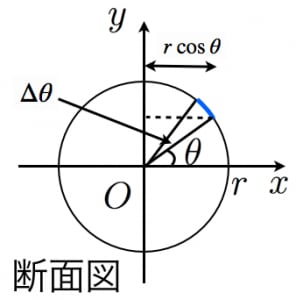
球の体積と表面積を積分で証明 高校数学の美しい物語
数値積分により円の面積を計算 Programming And Others
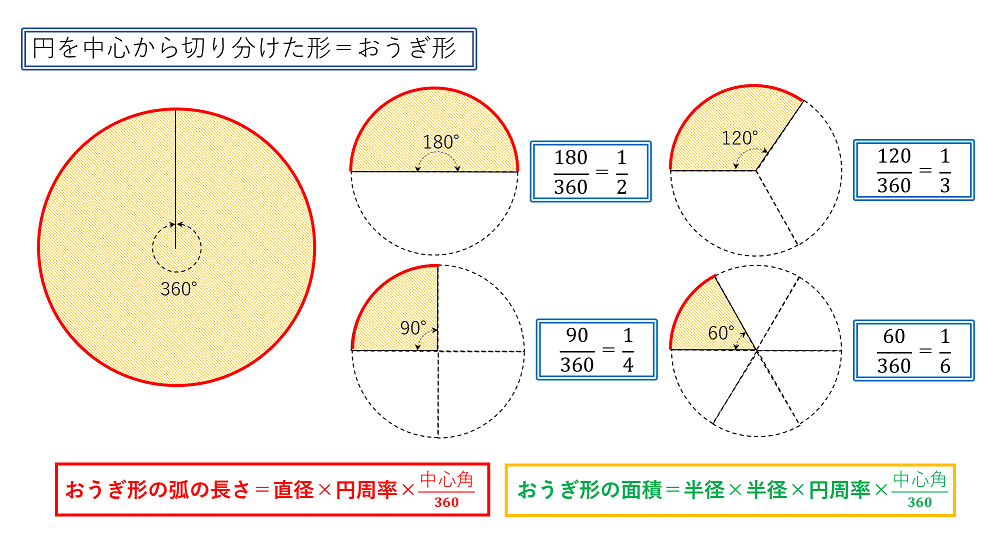
円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり 中学受験ナビ
子供に説明できる 円の面積の公式 の証明 働き方 学び方 Nikkei Style
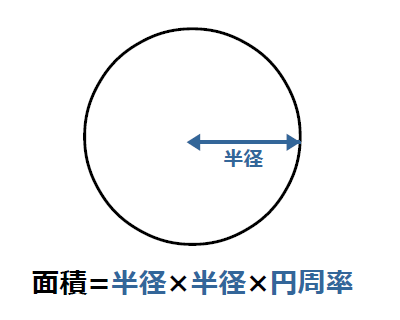
円の面積計算 ゆるゆるプログラミング

弓形の面積 九霄の彼方

球の体積 球の表面積の公式の導出 積分 優技録

2 いろいろな図形の面積 数学 積分法 オンライン教科書

数学を楽しむ 面積分
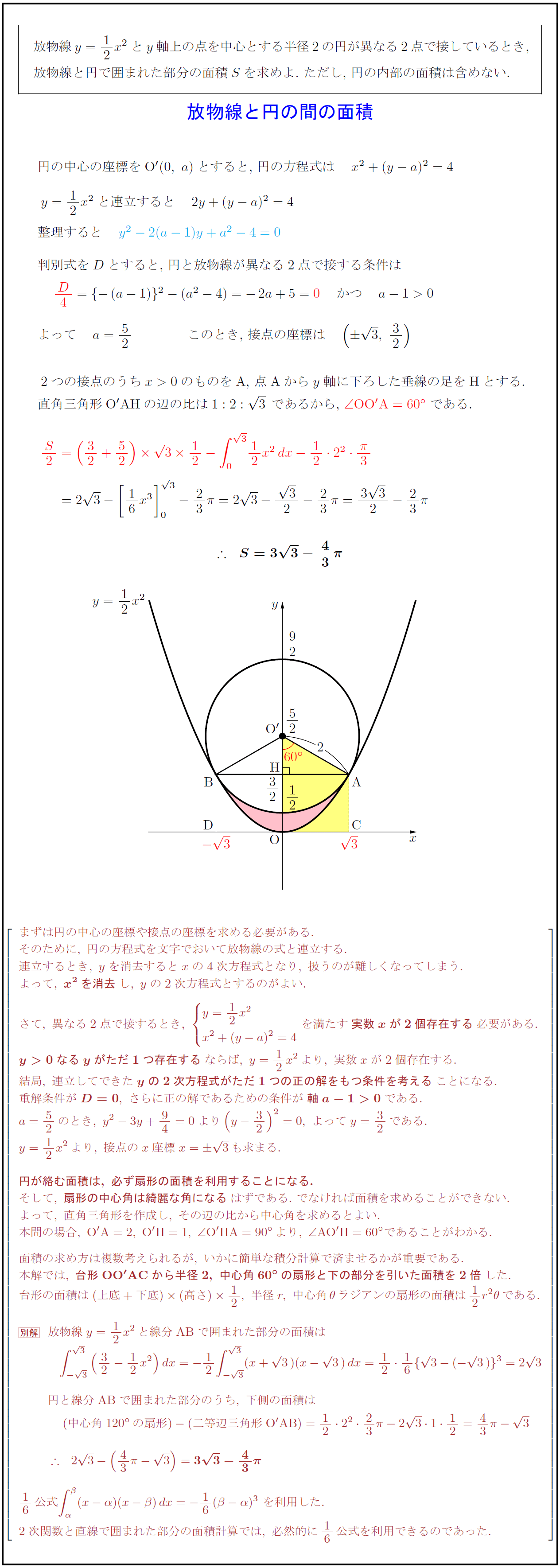
高校数学 放物線と円の間の面積 受験の月
48s96ub7b0z5f Net Houbutsusen En Menseki
円と放物線に囲まれた面積 微分法と積分法 おおぞらラボ

2つの円の一部が重なった図 2つの同じ大きさの円の一部が重なった状 数学 教えて Goo

楕円の面積公式の3通りの導出 高校数学の美しい物語

6年算数 円の面積 なぜ 半径 半径 円周率になるのか 解説します Youtube

6年算数 円の面積 なぜ 半径 半径 円周率になるのか 解説します Youtube

面積の求め方 計算公式一覧

高校数学 正十二角形の周長と面積 多角形の求積の原則 受験の月
Q Tbn 3aand9gcs Xtyzqnagm5fvlsj2 Svfjuvpiq0hmpic0h Tnnzokx7vf3pb Usqp Cau

光が丘オープンソースクラブ 数学ガール 積分を見つめて 第5章 円の面積を求めよう 円の内接n角形と外接n角形が円
なぜ円の面積 P 半径 半径 なのでしょうか 簡単に証明方法はあるのでしょうか Quora
面積を求める

弧で囲まれた図形の面積について 画像のような2つの円が互いの中心点 数学 教えて Goo

数学3 定積分の置換積分 高校数学に関する質問 勉強質問サイト

2 いろいろな図形の面積 数学 積分法 オンライン教科書
Q Tbn 3aand9gcsbv7rmb8 Mdykwz0agzwan5gkpn Jkfuaoelgqpjzngkhkz8gk Usqp Cau
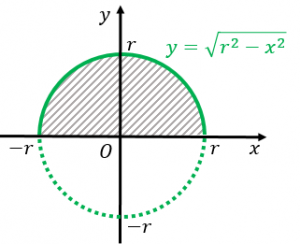
円の面積を積分で計算する2通りの方法 具体例で学ぶ数学

円の面積の求め方 公式と計算例
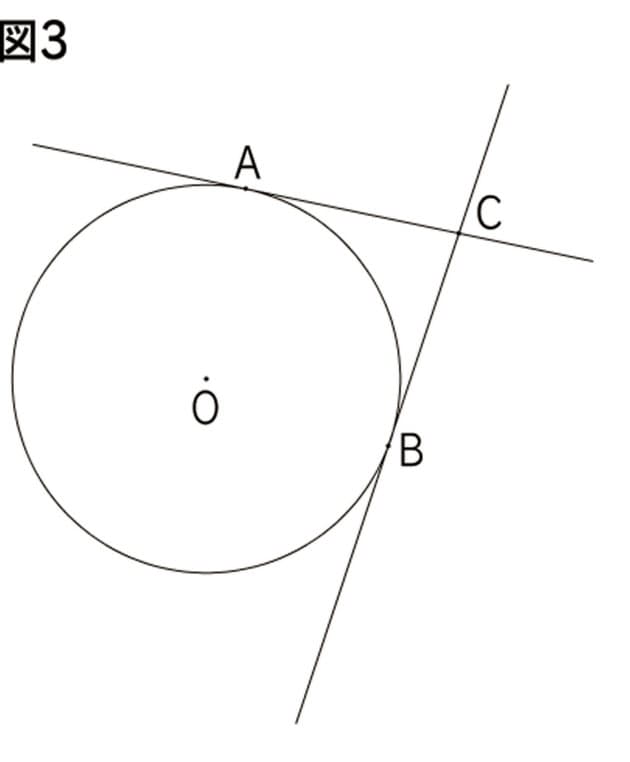
子供に説明できる 円の面積の公式 の証明 働き方 学び方 Nikkei Style

定積分と面積2 円の面積を3種類の方法で求めよう Youtube
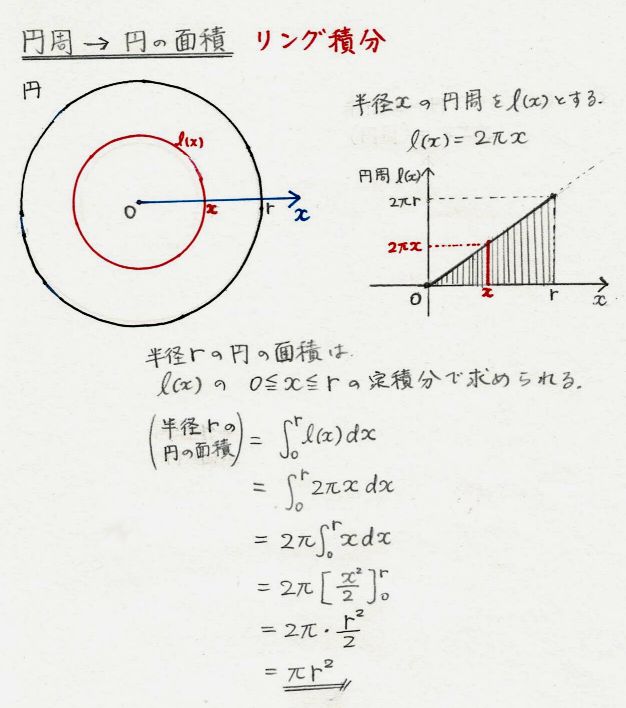
数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ
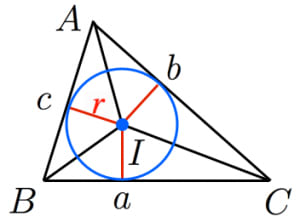
内接円の半径と三角形の面積 高校数学の美しい物語

高校数学 定積分と面積 2 問題編 映像授業のtry It トライイット

2 16 面積分
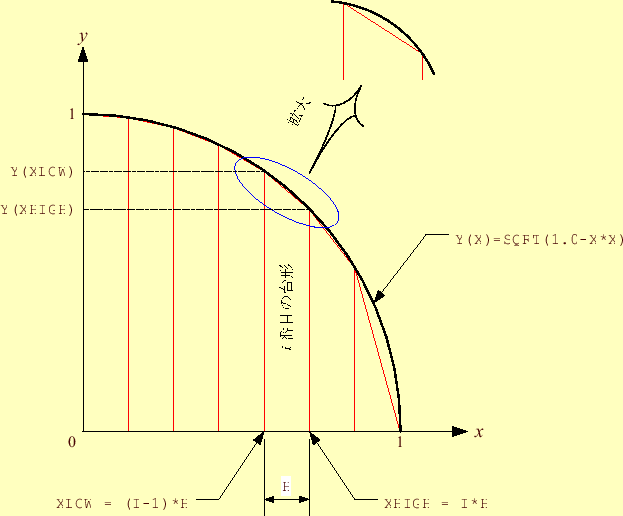
3 円の面積 数値積分の台形公式
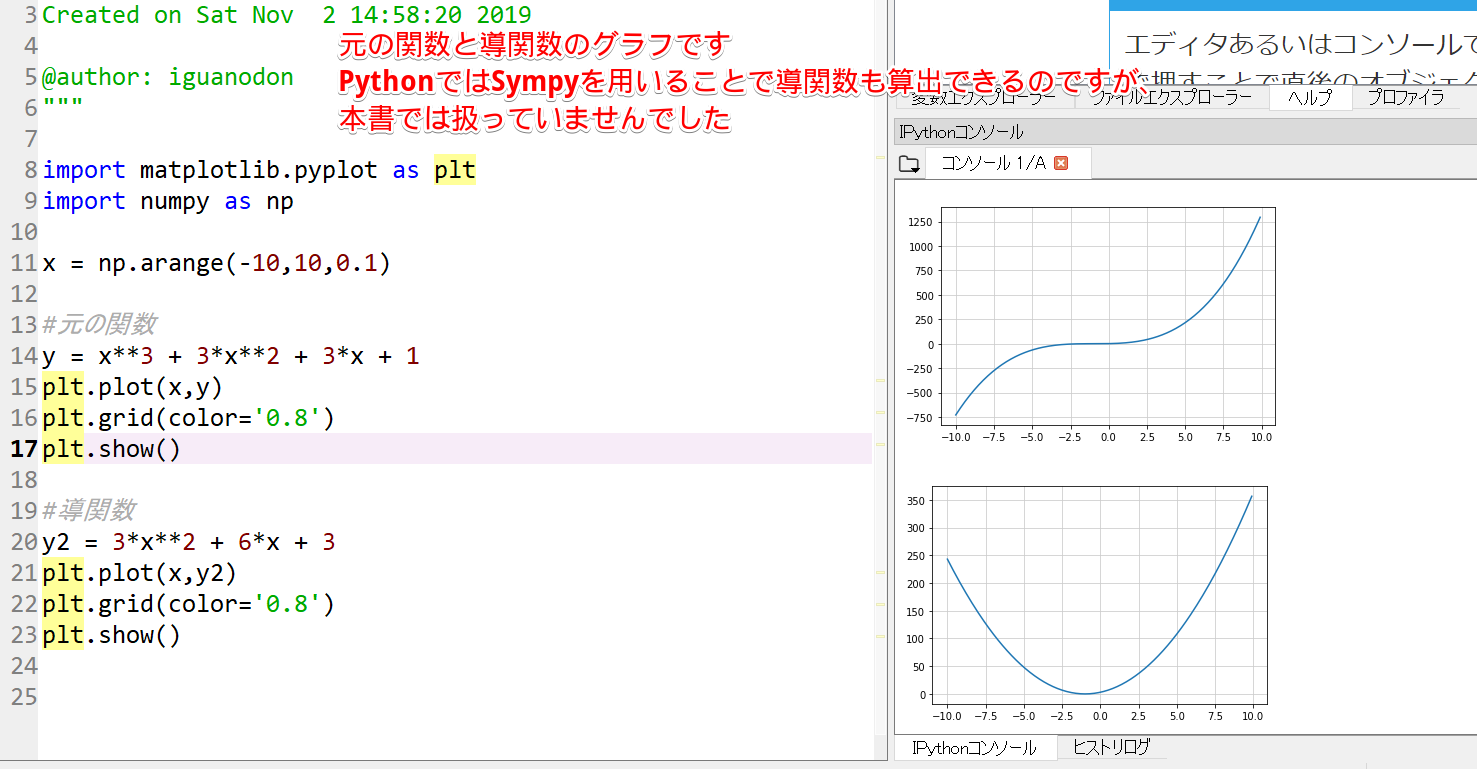
Pythonで学び直す高校数学 8章 微分 積分 アパトサウルスのブログ 令和な日々改め
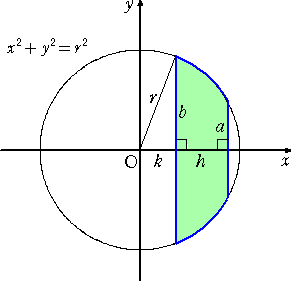
球帯と球冠
子供に説明できる 円の面積の公式 の証明 働き方 学び方 Nikkei Style

円の面積 練習応用 Youtube
J8awcdikobc Pm

中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット

誤答から学ぼうシリーズ 回転体の体積 ほのぼの数学頑張ろう

標準 おうぎ形と正方形の面積 なかけんの数学ノート

ジョゼフ アンリ على تويتر 見掛け倒しの問題ですね 定積分の表す部分の面積が円の面積の1 4でしかないですね
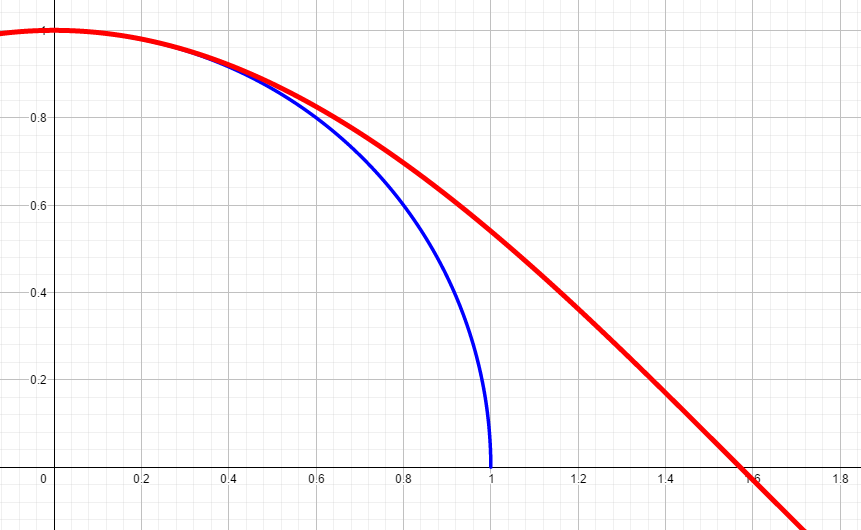
置換積分のイメージ 極小をさらに縮める キソカラ
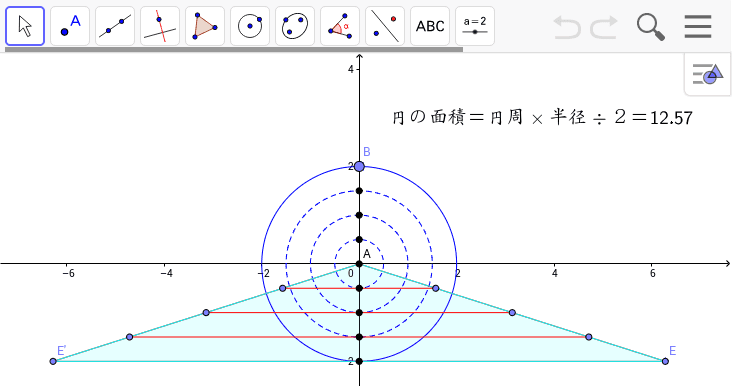
円の面積の求め方 Geogebra

円の面積の求め方と覚えるコツ なぜ半径 半径 3 14になるか アタリマエ

小6 円 円の面積の求め方 日本語版 Youtube

波線の式がなぜ円の面積を表しているとわか 高校数学に関する質問 勉強質問サイト

高校数学 楕円と円の関係 楕円の面積 受験の月
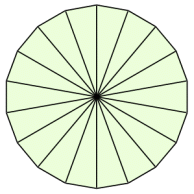
積分 円の面積の再考 大人が学び直す数学

高校数学 円の伸開線の面積と長さ 受験の月

数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ
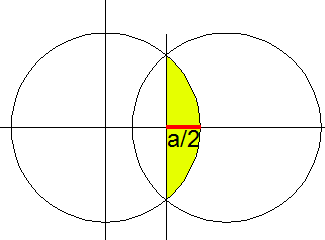
くろべえ 卵焼きの失敗と 2円の重なり部分の面積
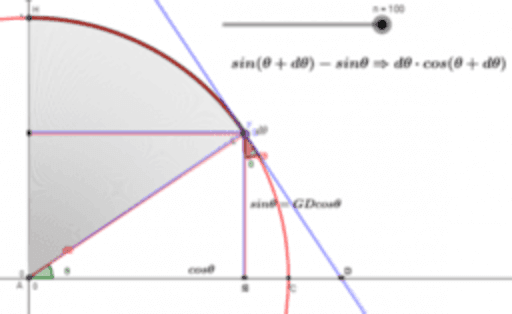
面積と積分 Geogebra

002 9bdr1ekigm

半円を回転させる面積の問題 プリントを使って自分で解こう
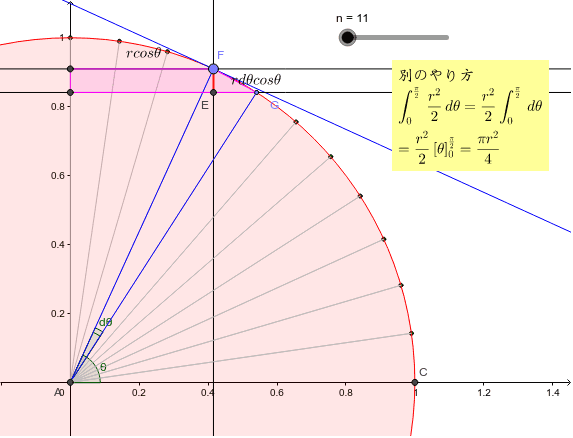
円の面積2 Geogebra
Search Q E5 86 86 81 Ae E6 96 B9 E7 A8 8b E5 8f Tbm Isch
下記の画像で 弧長を半径で積分すると扇形 円 の面積になる 水 Yahoo 知恵袋

高校数学 楕円の面積と回転体の体積 受験の月
三角形の面積を外接円の半径を使って求める Schoolmath S Diary
面積を求める

数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ

円の面積 Java実験室
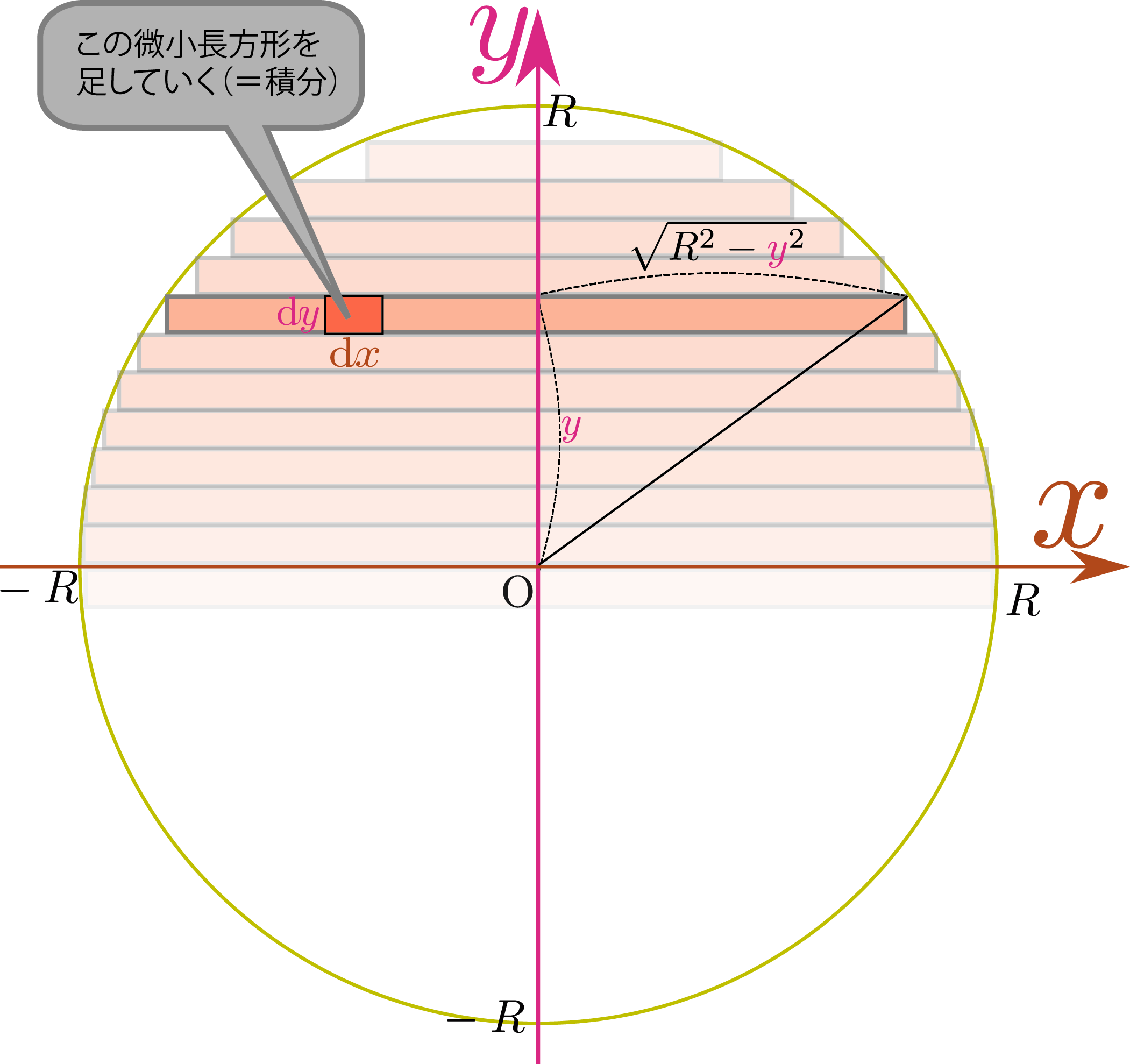
面積分
円と帯の共通部分の面積 Den Of Hardworking

はっぱ型 の図形の面積 身勝手な主張

円の面積の公式 算数の公式
六 輪 生 活 円の面積はなぜ半径 半径 Pなのか
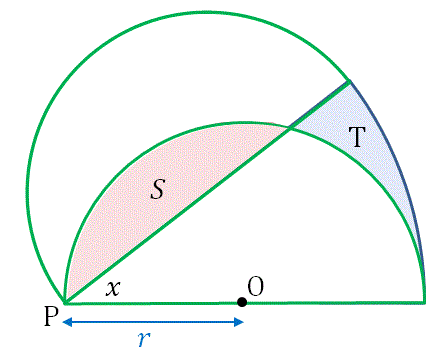
Excel Vba 数学実験室 面積が等しくなるように半円を回転させて回転角を求めます
工作4
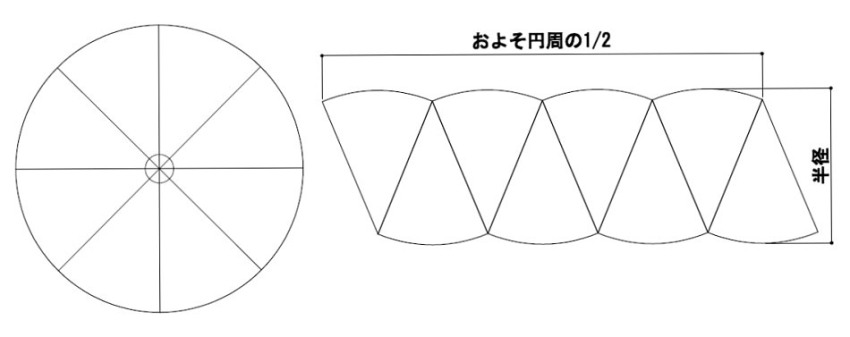
六 輪 生 活 円の面積はなぜ半径 半径 Pなのか
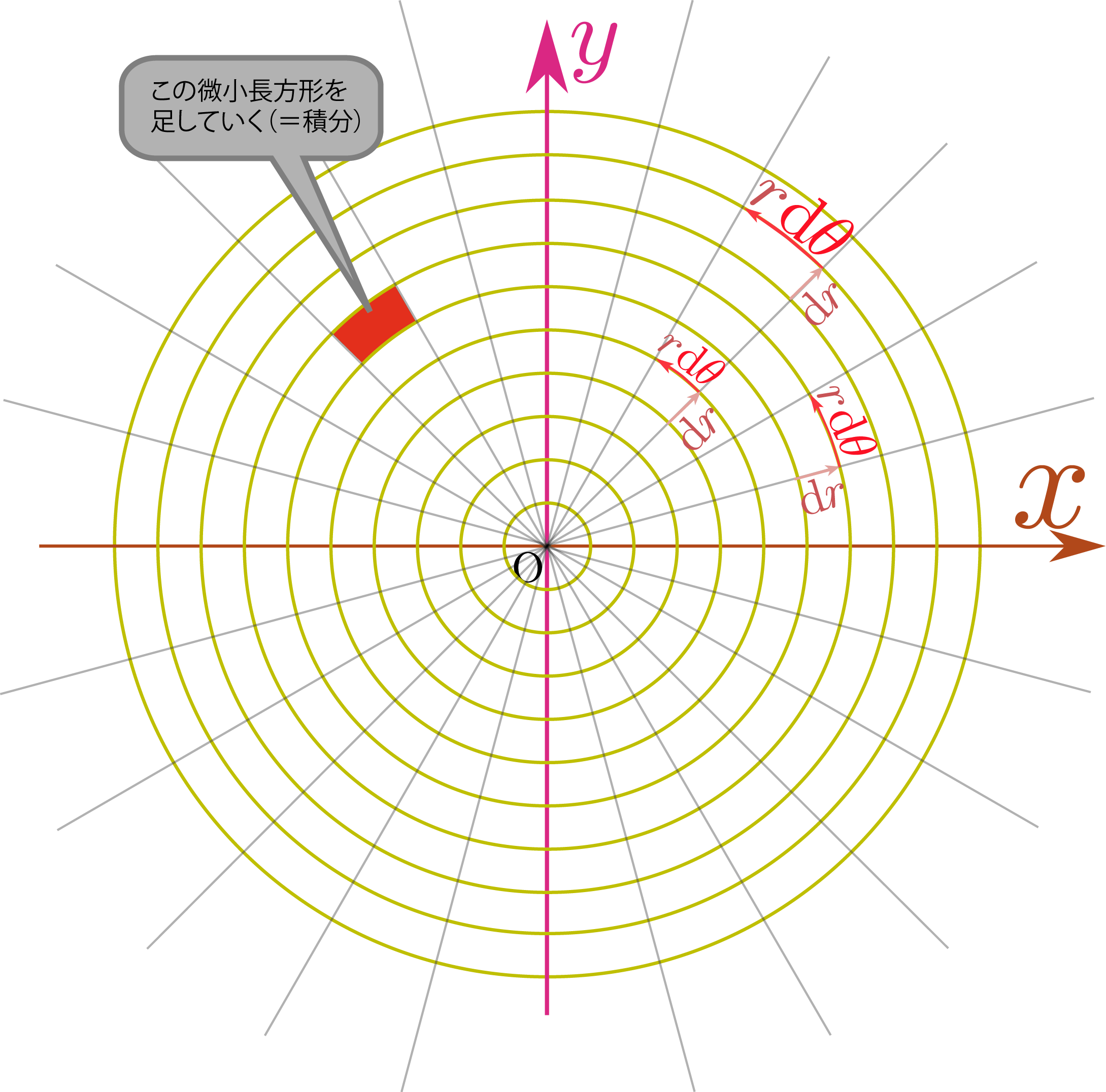
面積分

球の表面積と円の面積 数学 算数のq A 締切済み Okwave
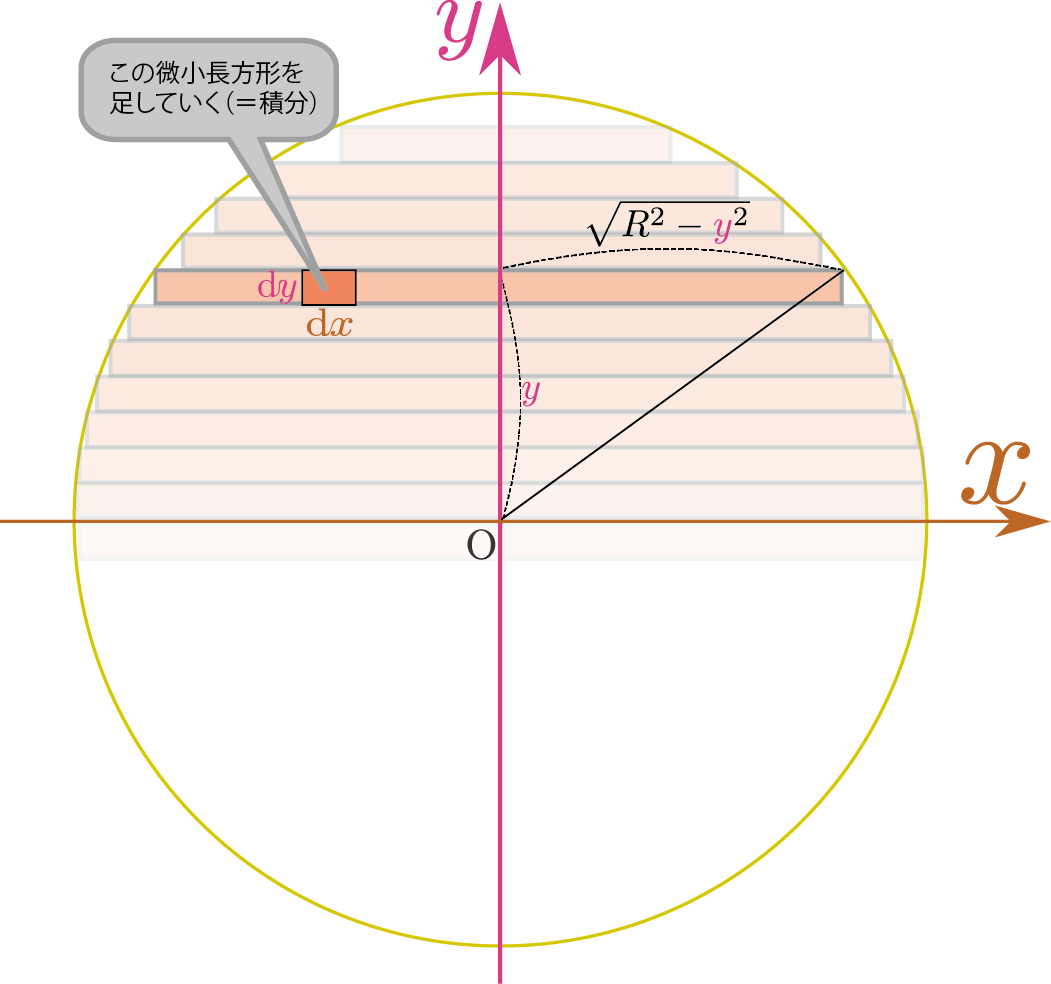
2次元での積分

円の部分面積と部分円周を教えてください 添付にある円のcの面積と 数学 教えて Goo

円の面積の求め方と覚えるコツ なぜ半径 半径 3 14になるか アタリマエ

中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット
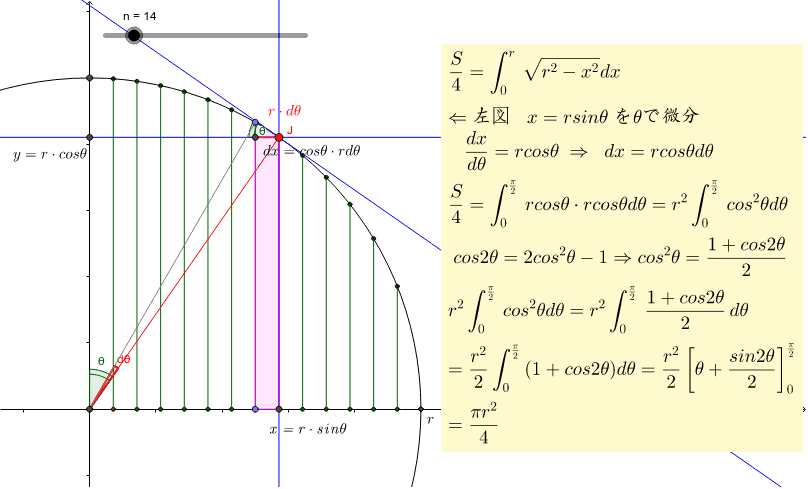
円の面積 置換法の意味 Geogebra
勉強しよう数学 円の面積を積分で求める
気まぐれ Net 図を用いた円の面積の求め方 公式を使わずに

abcの面積 その内接円の面積 の最小値 身勝手な主張

積分を用いた円の面積公式の証明について 数学 算数のq A 解決済み Okwave




