五角形 の 内角
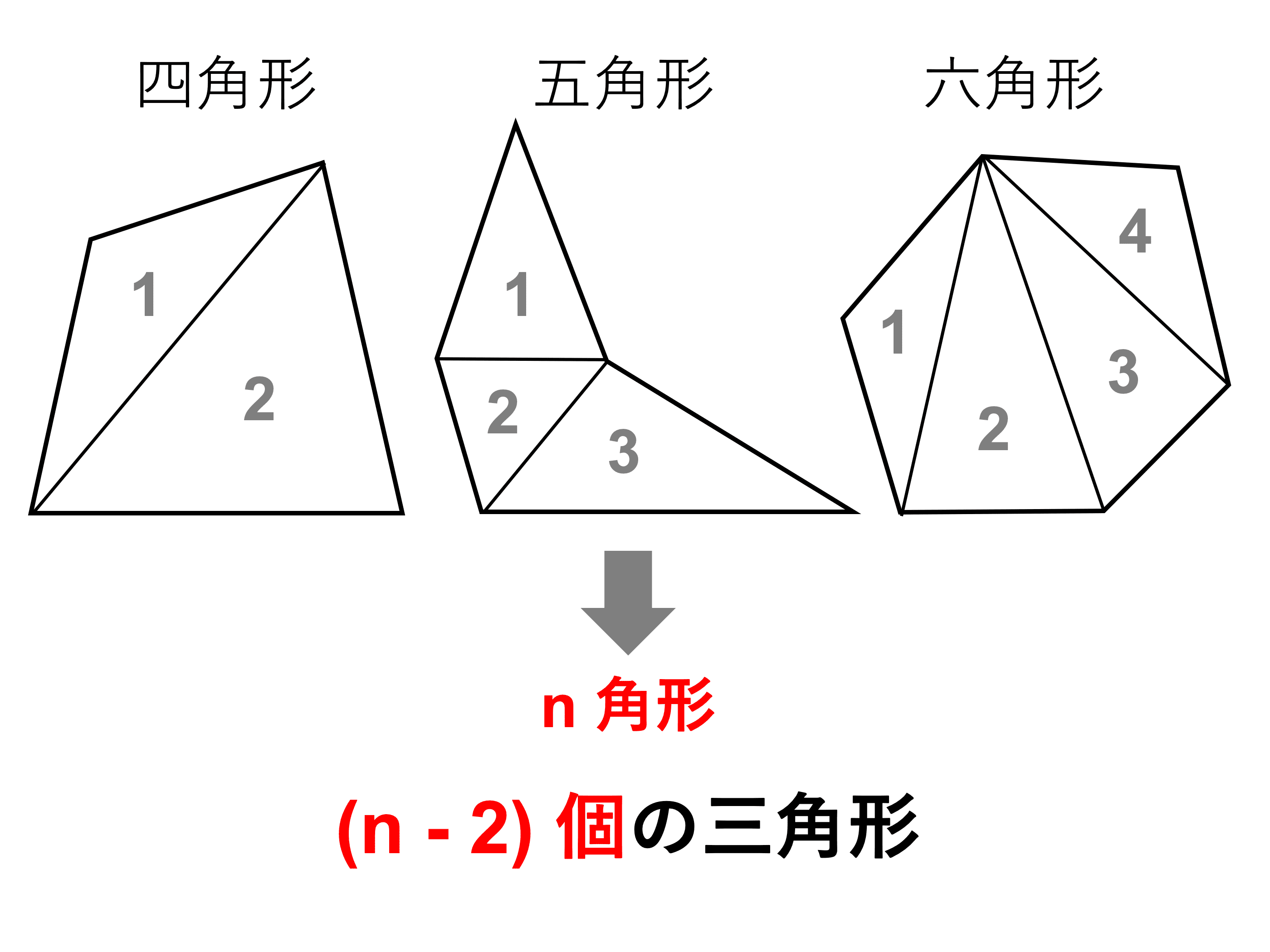
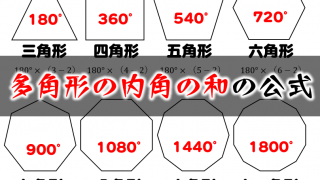
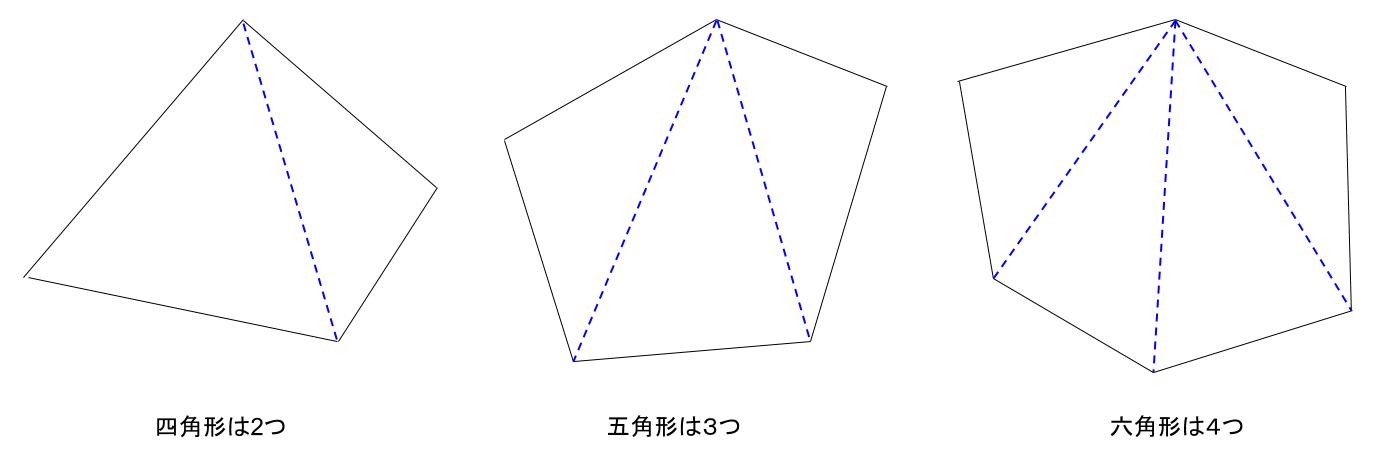
多角形の内角の和と対角線の数の問題です。 公式を覚えておけば出来ますが、最近は公式の導き方を問うことも増えています。 丸暗記するのではなく、多角形の性質をしっかり確認して公式を使うようにしていきましょう。 多角形の内角の和 六角形の内角の和を求める場合 上のように4つの.

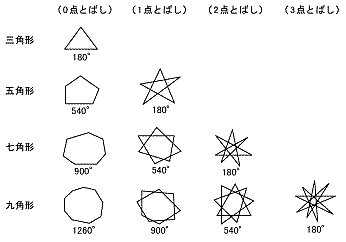
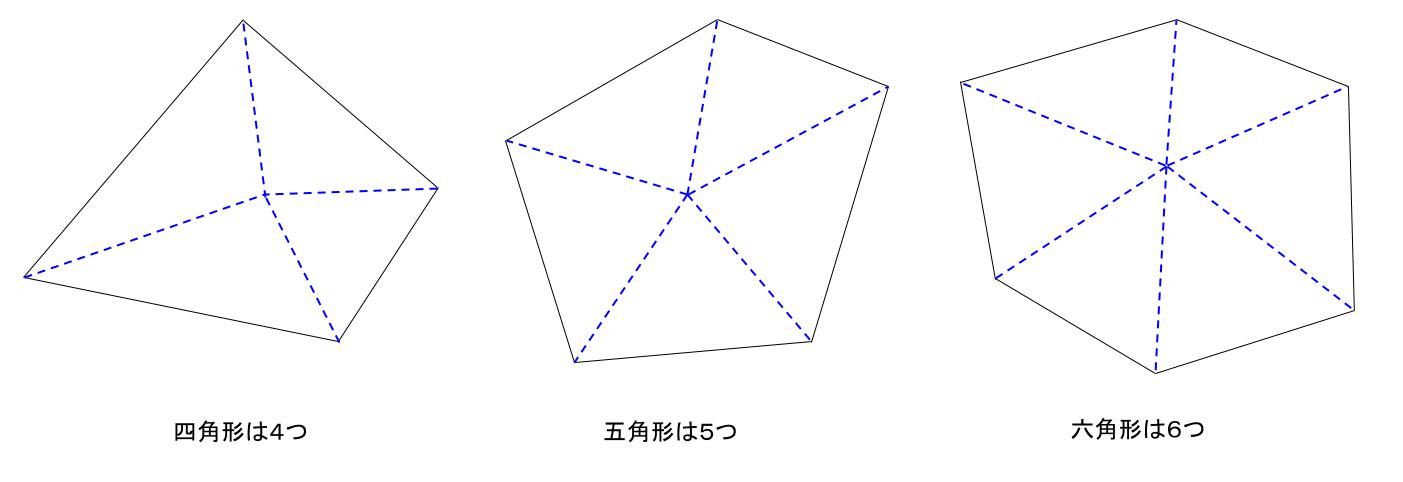
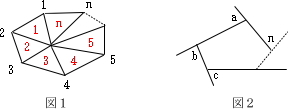
五角形 の 内角. ・ 「五角形」「六角形」「多角形」の・探究的な活動 ことを理解している。 4 定義を知る。 ・説明する活動 / ・ 五角形,六角形の内角の和を,三 8 角形に分割して調べ,多角形の内角 の和について表にまとめる。 ・ 多角形の内角の和のきまりを考え る。. 多角形の内角の和 目標時間 名前 五角形の内角の和のついて、 にあてはまる数を 書きましょう。 考え方1 1つの頂点から対角線をひくと、 三角形が 個できます。 三角形の内角の和は ° ° 考え方2 五角形の中央の点oと頂点を結ぶ 三角形が 個できます。. 2-4-1 星型多角形の内角の和 教材(問題場面) 図のように5つの点A,B,C,D, Eがある。.
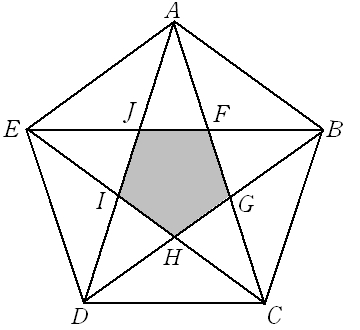
形や五角形の内角の和 を求めることができ る。 四角形の4つの角の大 きさの和は何度になる でしょう。 ①四角形の内角の和を三角形の内角の 和の求め方や三角形の性質を用いて 求める。 ②四角形の内角の和の求め方を活用 し、五角形の内角の和を求める。. る。星型五角形を2つの三角形ACDと三角形B FEに分ける。それらの内角の総和360°から, FCDの内角の和180°を引き,星型五角形の 内角の和180°を求めることができる。 f ウ 五角形の外角の和を利用する 図のように,星型五角形の5つの角をそれぞれ. N 角形の対角線の本数を m 本としたとき n = m が成り立つのは n = 5、すなわち五角形だけで.
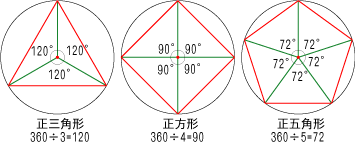
・多角形の内角の性質を調べる。 ・いろいろな多角形の内角の和を求 める。 思n 角形の内角の和が180°×(n-2)になること を帰納的、演繹的に導くことができる。 知多角形の内角を求めるいろいろな方法を理解し ている。 1. また、中学へのつなぎとして、「 角形の内角の和は?」と問いかけ、一般化も可能となります。 他の三角形でも言えるか?四角形では?五角形では? まとめ:三角形の3つの角の大きさの和は180°になる。 「問い」の発展. 三角形の角度の和を次々に足していけば、多角形の内角の和が求められます。 Dividing a regular hexagon by its diagonals, we get six equilateral triangles.
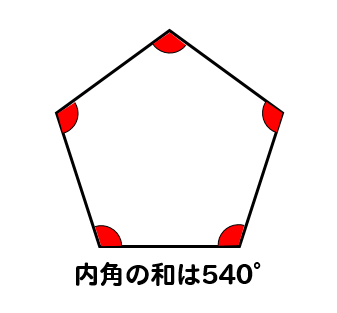
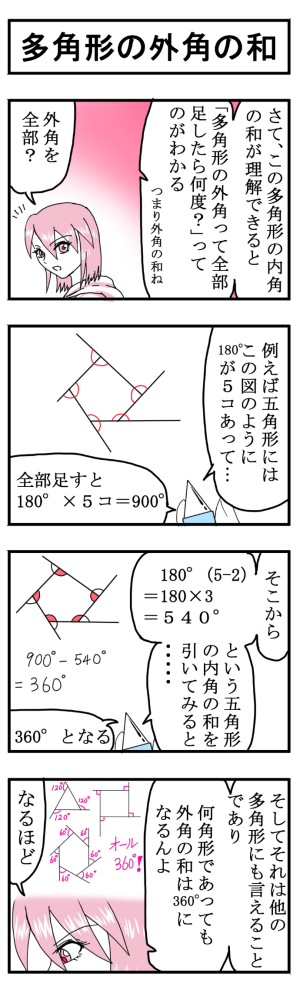
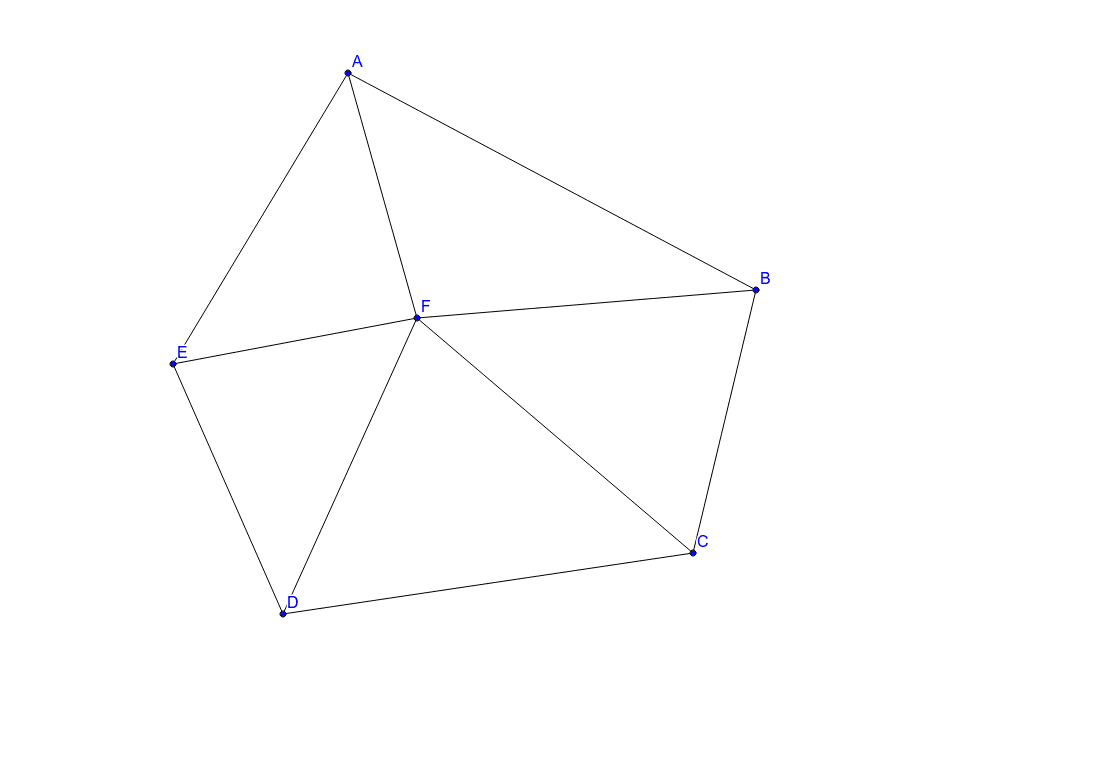
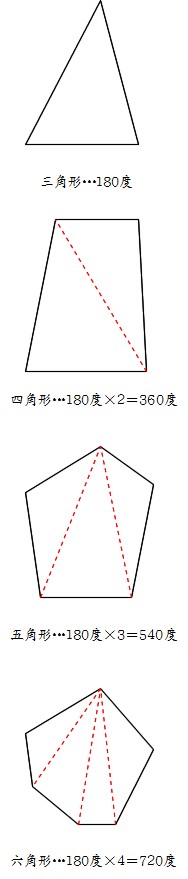
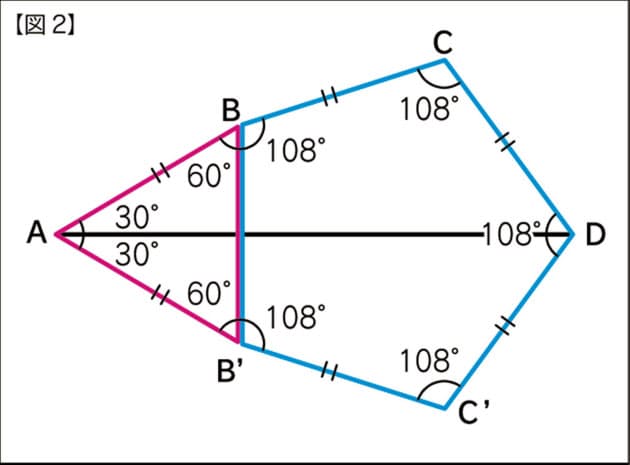
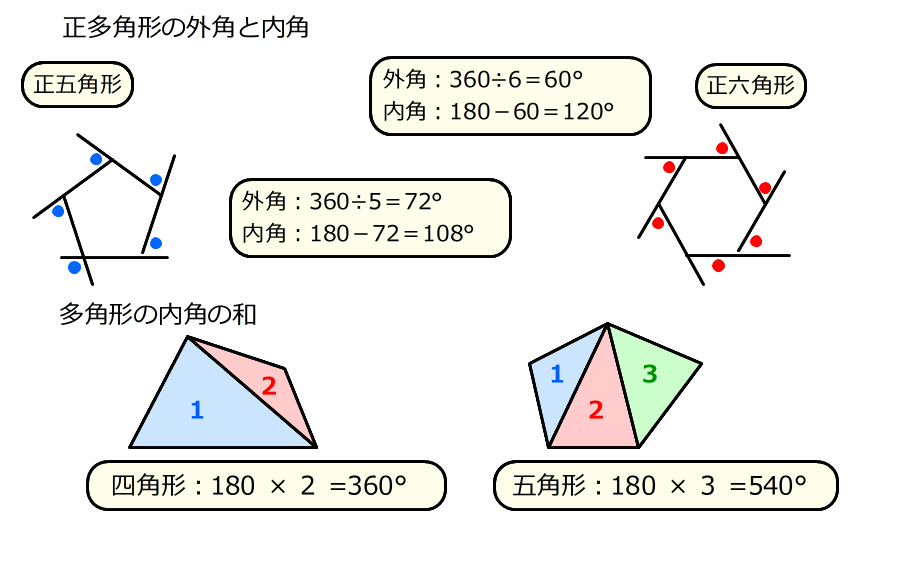
五角形の内角の和は「540°」 ってことさ! なんで内角の和が540°になの?? 公式をつかえば1秒ぐらいで計算できそうだけど、 そもそもなんで「540°」になってるんだろう?? チョー気になるよね笑. まずは角度に注目。 内角の和が540°なので、1つの内角が 108° 。 対角線を引いたら内角が 3等分 されます。 分解してできる三角形の内角は、 36°、72°、108°の3種類 。 そして、 36°:72°:108°=1:2:3 になっています。. 五角形,六角形の内角の和を三角形に 分けて調べ,多角形の内角の和につい て表にまとめる。 考三角形の内角の和を基に,多角 形の内角の和を三角形に分け て求める方法を考え,説明して いる。 知多角形の内角の和は,三角形に 分けることによって.
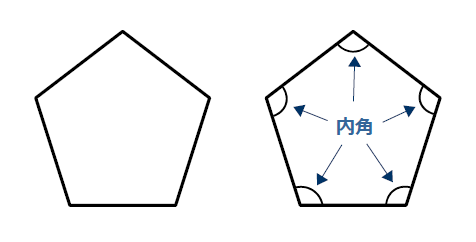
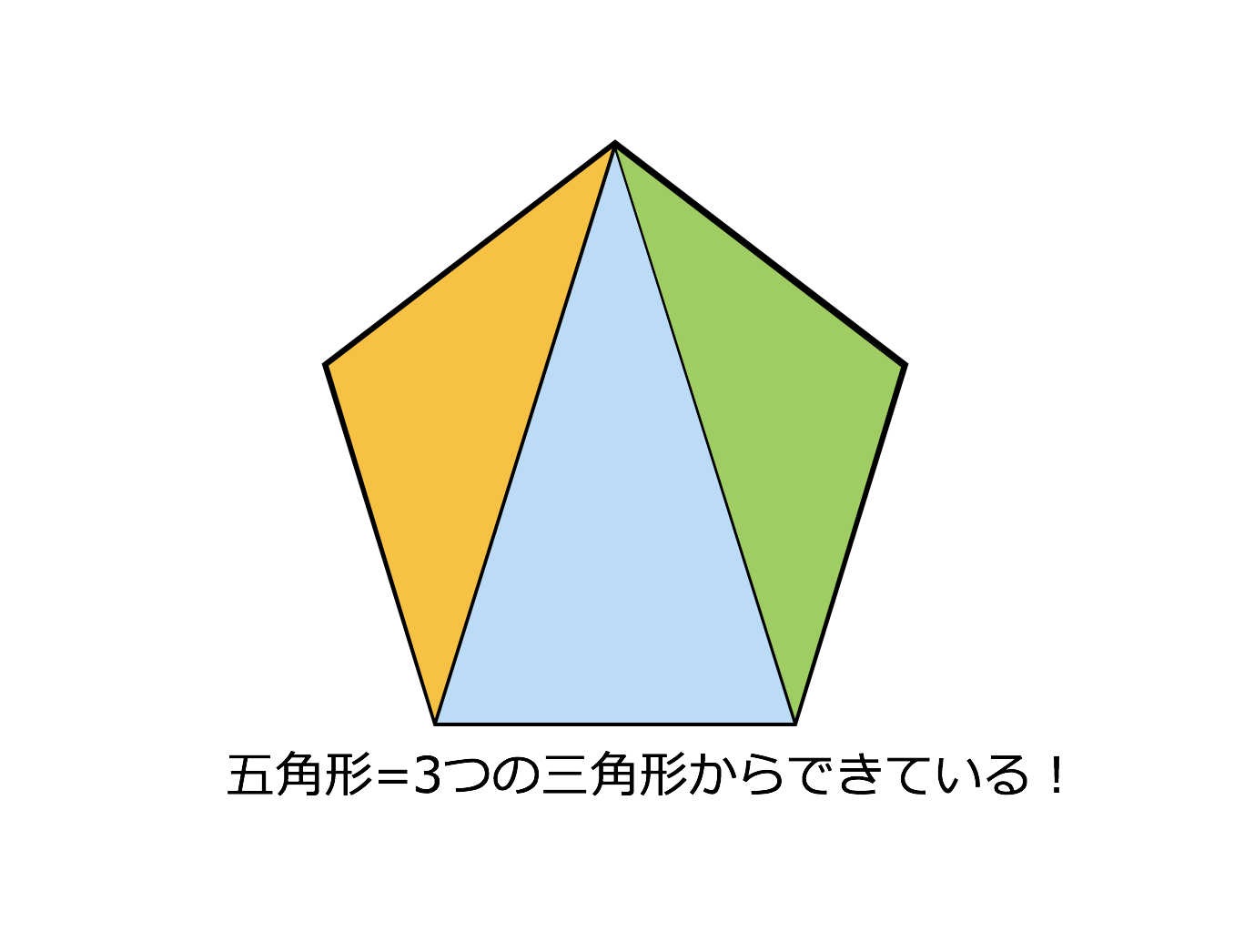
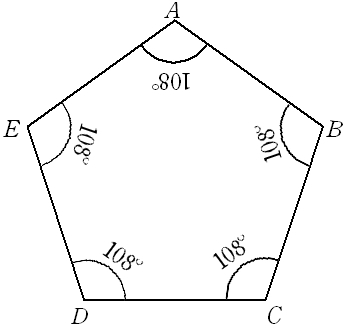
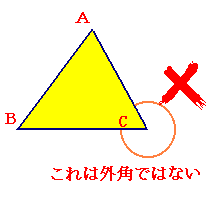
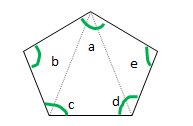
「五角形や六角形の内角の和を求 める方法を考えよう」 <五角形> ⇒三角形が3つできるから <六角形> 生徒は板書,あるいはノートに記入しながら発表する。 ⅰ.対角線が1本しか引けない。 対角線が引けていない四角形に目を向け させる。. 内角とは、多角形の隣り合った2辺がつくる角度のうち、多角形の内側の方の角度です。 下の図は、五角形の 内角 を表したものです。 5つの角に1つずつ 内角 があります。. 正五角形の作図 正五角形を自分で作図できるようになってみましょう。 正五角形とは, 定義①すべての辺の長さは等しく, 定義②すべての内角の大きさが等しい 図形の中で,辺および頂点の数が5個のもの。 ということにします。ただし,正5 2.
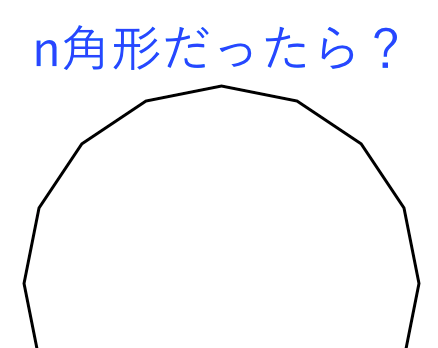
中学受験専門プロ個別指導塾ノア 算数 角度 多角形の内角の和 - Duration:. 右の表のように,n角形を三角形に分けると, n−2個の三角形になるから, 内角の和は 180°×(n−2) になる. ≪例≫ 三角形の内角の和は180° 四角形の外角の和も360° 五角形の外角の和も540° …. 正n角形の内角の大きさの求め方画像の説明がまったく理解できないのですが、式の意味を教えて下さい。多分 133ページには、こんなようなことが書かれていた筈です。四角形の 一つの頂点から 他の頂点の線を引くと、2つの三角形が出来ます.
「五角形」、「六角形」や「多角形」 の用語とその定義を理解し、それぞ れの形の内角の和を求めることが できる。 ・ 五角形の内角の和を工夫して求 め、540°であることを説明する。 ・ 多角形の内角の和を表にまとめ る。 児童が説明する算数的活動. この記事では、多角形について、外角の和や内角の和の公式、面積や対角線の本数の求め方について解説していきます。 また計算問題の解き方もわかりやすく解説していくので、ぜひこの記事を通してマスターしてくださいね! 目次多角. タヌキ 正5角形の内角の和を計算すると 5角形は三角形3つに分けることができるから 180×3=540°となります。 キツネ 正5角形は5つの等しい内角でできていて この5つの角度の和は、540°だから、 1つの角は.
しろいと感じている生徒が多いことがわかる。また、導入で扱った星型五角形の解き方に興味を持ち、 質問してくる生徒も何人かいた。 4,指導計画 平行と合同 第1次 多角形の内角と外角 ①多角形の内角と外角 3時間 ②平行線と角 4時間. さっそく、正五角形の内角を計算してみよう! 正五角形は頂点が5つあるから、 さっきの公式のnに「5」をいれるだけでいいんだ。 すると、 180 × (n-2)/n = 180×(5-2)/5 = 108° になるね。 つまり、 正五角形の内角の大きさは「108°」ってことさ。. (内角)+(外角) =180° (外角) =180°− (内角).
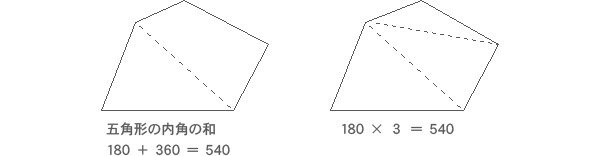
五角形は三角形3つに分けることができ 、三角形の内角の和は\(180^\circ\)であるので 180^\circ \times 3 = 540^\circ となります。. 多角形の内角の和は求められないでしょうか? そんなことはありません。 忘れてしまった場合は、前項で使用したこんな表を自分で作成してみましょう。 三角形、四角形、五角形辺りまでで、. 中学受験専門プロ個別指導塾ノア 4,990 views 5:15.
正五角形は、各辺の長さが等しく、内角も108°(中心角は72°)と一定な五角形である。 辺の長さを a とすると. また,星形五角形や星形七角形は一筆書きでかけますが,星形六角形や星形 八角形のときには一筆でかけない場合があります。星形が一筆書きでかける のはどんな条件のときか,調べてみましょう。 星形多角形の内角とは,多角形. ・5つの頂角を1つの三角形の内角に集める。 ・五角形の内角・外角を利用する。 ・その他 ・自分の解き方を説明している。 ・友だちの解き方を聞き,納得したり,新しい方法を考えている。 ・180度と答えた生徒が多い。.
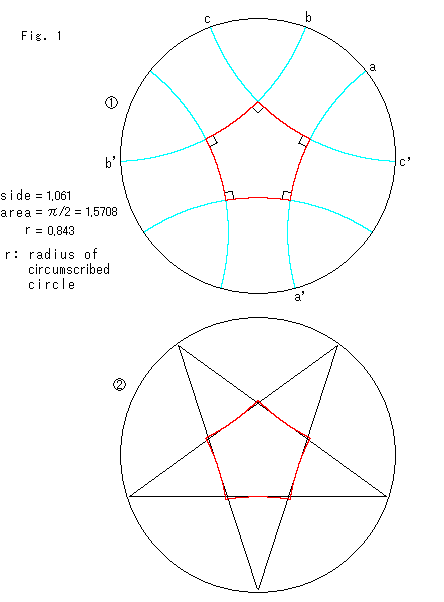
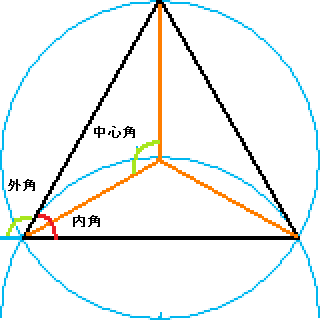
三角形の内角と外角 $ ABC$ において,$\angle A,\angle B,\angle C$ を,$ ABC$ の内角といいます. また,下図の $\angle ACD$ や $\angle BCE$ のように,一つの辺とその隣の辺の延長がつくる角を,外角といいます. さて,三角形の内角と外角について,次の重要な事実が成り立ちます.. 面積 = = + ≃ 内接円の半径 = 外接円の半径 = = + 正五角形の作図.

この問題の答えはイなんですけど どうしてそうなるのかが分かりません Clear
2
正多角形の1つの内角 外角を求める方法を問題解説 数スタ
五角形 の 内角 のギャラリー

多角形の内角と外角 思考力を鍛える数学

Motoの独り言 正五角形を書く方法であるが 証明が難しい

Q Tbn 3aand9gcq T29owmxlphfpfncusbefemmxkyhh4yhb1a Usqp Cau

正五角形の1つの内角の大きさ 単位 Deg 17年12月31日の人物のボケ ボケて Bokete

十五角形 Wikipedia
図形の調べ方 N角形について 内角の和を求める 苦手な数学を簡単に
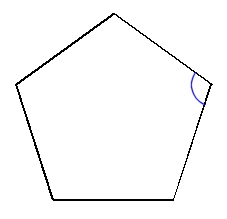
正五角形の内角 外角
2
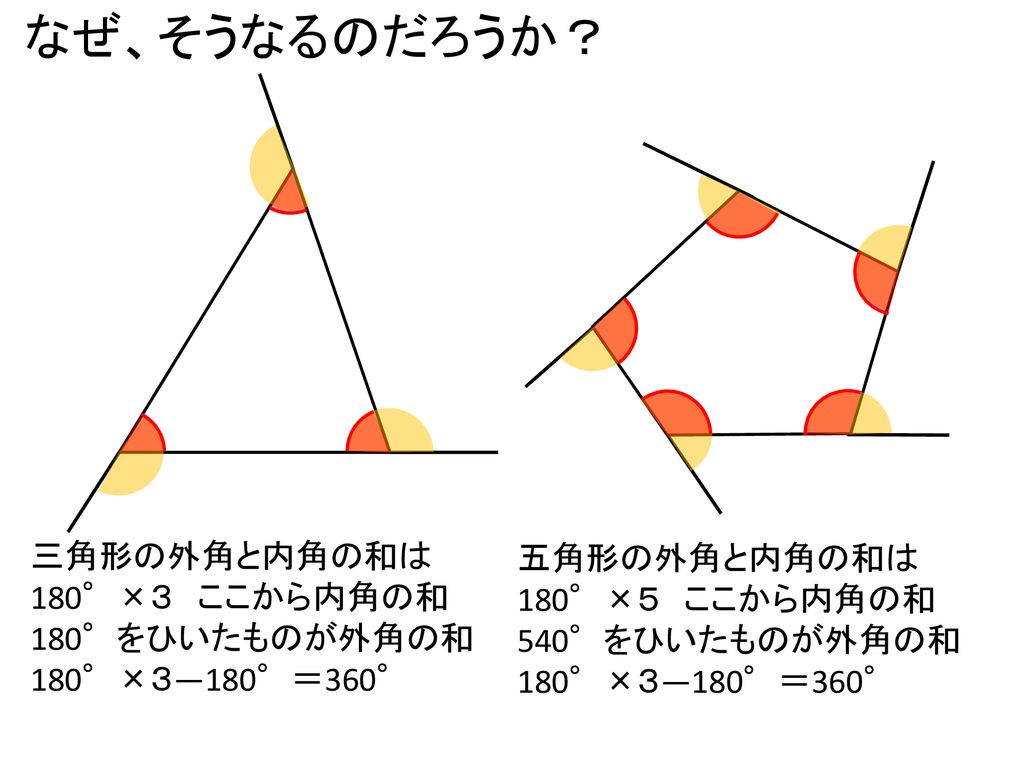
多角形の外角の和 凹型四角形の角 星形五角形の内角の和 Ppt Download
5角形の内角の和
2

無料 中2数学 標準問題 解答プリント 224 図形4 三角形の合同条件
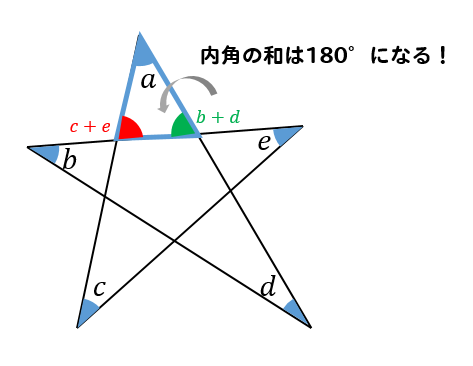
星形の角度 内角の和の求め方を問題解説 数スタ

五角形 Wikipedia
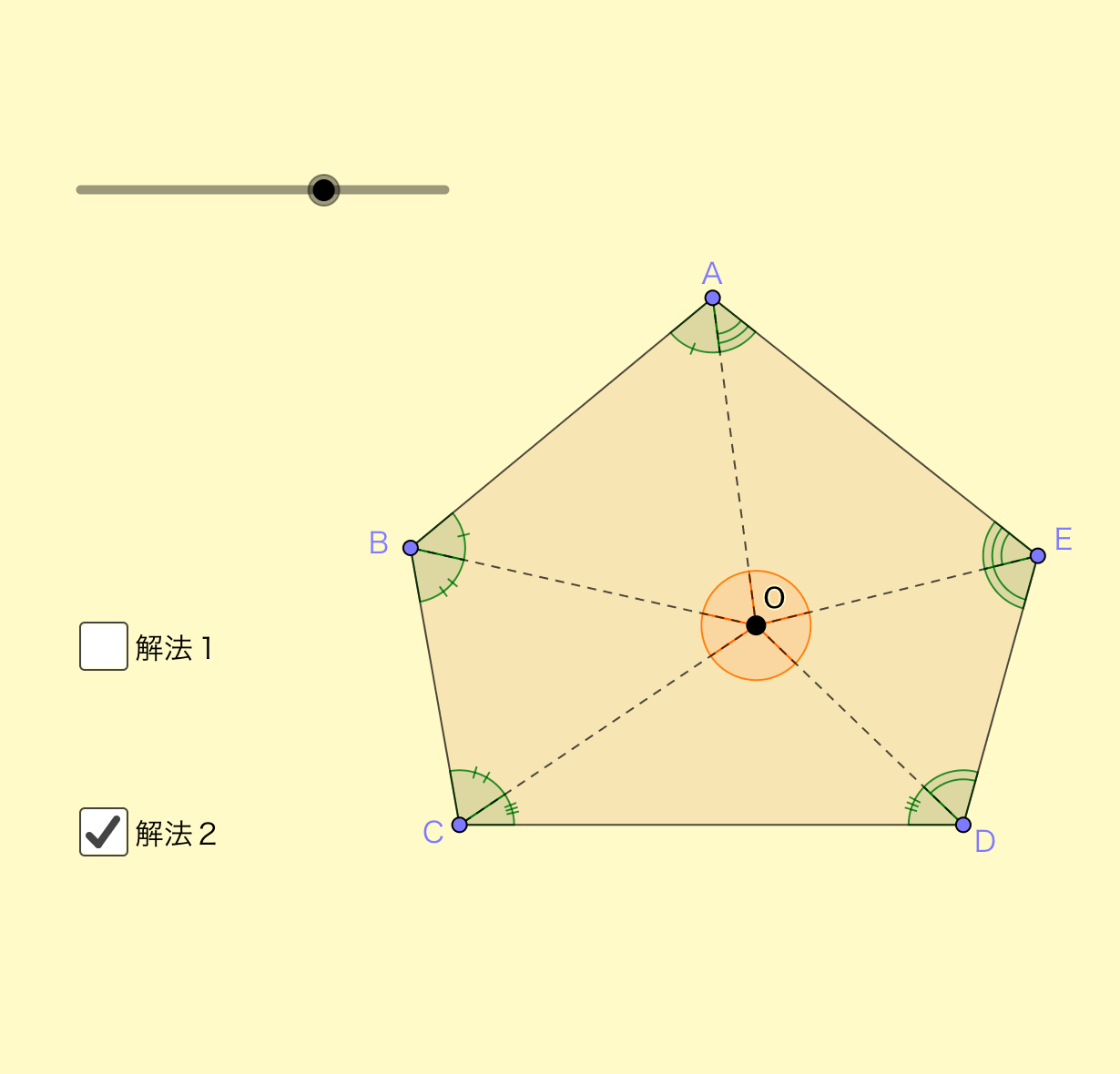
五角形の内角の和の求め方 久保塾 今治市の学習塾

多角形とは 内角の和の求め方を簡単に解説 高校生向け受験応援メディア 受験のミカタ
五角形 の 対角線 は 何 本 対角線の長さ 本数の求め方とは 公式を使って一瞬で計算しよう
多角形とは 外角の和 内角の和の公式や 面積や対角線の本数の求め方 計算問題などを徹底解説 受験辞典

五角形の内角を求める問題です 数学 算数のq A 解決済み Okwave

多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学
重なる形と図形の角を調べよう 第5学年 小学校 算数 My実践事例 日本文教出版

動画で学習 2 多角形の角 数学
n角形 多角形 の内角の和の求め方

第5回 別解を考える 解答 解説 連載一覧 さぽナビ Z会

課題学習の指導 数学

多角形の内角の和 外角の和の公式 多角形 和 数学

簡単公式 五角形の内角の和を3秒で計算できる方法 Qikeru 学びを楽しくわかりやすく
Core Ac Uk Download Pdf Pdf
内角 ゆるゆるプログラミング
3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ
茗渓予備校 科目別データベース
直角正五角形

多角形の内角の和 算数の公式覚えてますか

切ってはって算数力 正2分の5角形 朝日新聞デジタル

正五角形の作図法 数理女子
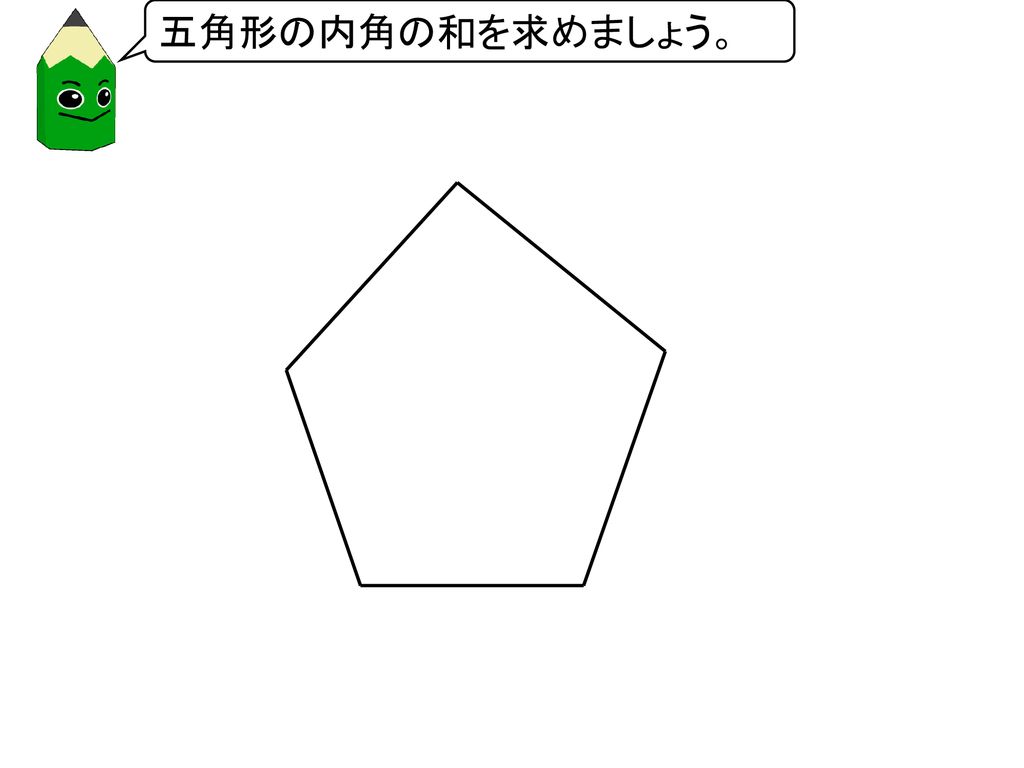
三角形や四角形ではない図形の 角の大きさの和を求めよう Ppt Download

多角形の内角の和 は何度なのか を説明します おかわりドリル

高校入試 英語 数学 学習 平行と合同 多角形の内角と外角

多角形の性質 第2回 多角形の内角の和の求め方 算数パラダイス 中学受験プロ家庭教師hp
多角形 の内角の角度 計算ドリル 問題集 数学fun

中2数学 多角形の内角 映像授業のtry It トライイット

多角形の内角の和の公式を3通りの方法で証明する 具体例で学ぶ数学
2

正五角形に付随する角度と黄金比の関係 萌えとかプログラミングとか

中学数学 三角形の内角と外角の関係の利用

中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく
課題学習の指導 数学

多角形の内角の和の求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト

多角形の角 無料で使える学習ドリル

内角の和の公式 内角の和が1800 の多角形は何角形 中学や高校の数学の計算問題

無料 中2数学 標準問題 解答プリント 223 図形3 多角形の角
茗渓予備校 科目別データベース
数学得意な方お願いします 正五角形の1つの内角は何度になりますか その角度を求 Yahoo 知恵袋

多角形の内角の和の公式を3通りの方法で証明する 具体例で学ぶ数学

自然の中でのジオメトリ 正五角形 Adelfa グラフィック表現
五角形の内角の和 Geogebra

高校受験数学 図形と合同 Study Supporter
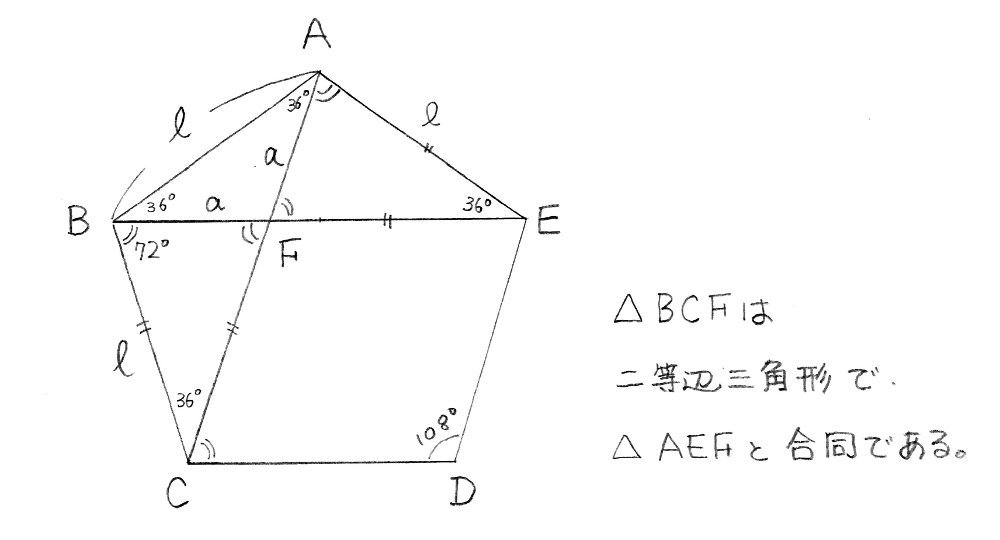
五角形5 辺と対角線の比 Wandering In The Woods

中2数学 多角形の内角と外角 練習問題と誰でもわかる解答

中2数学 多角形の内角 外角 図形の合同 ひっそりと物理や数学を解説する
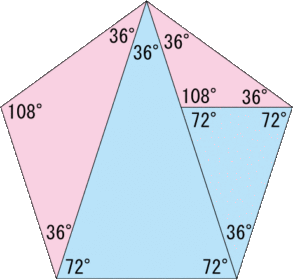
図形 正五角形の分解 父ちゃんが教えたるっ

中学2年生の数学 内角の和 外角の和の復習 塾講師が数学をやりmath
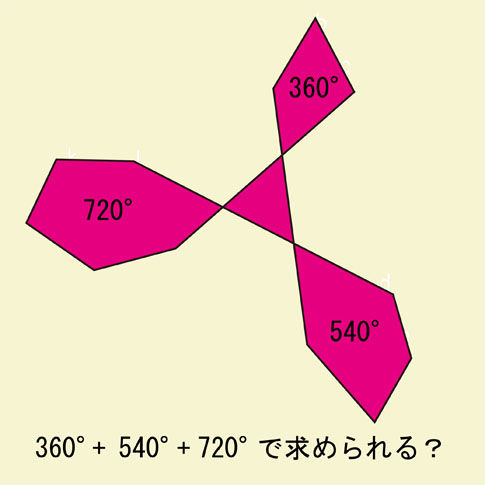
12個の角の和を求められますか 油断大敵を地で行く問題 秒刊sunday
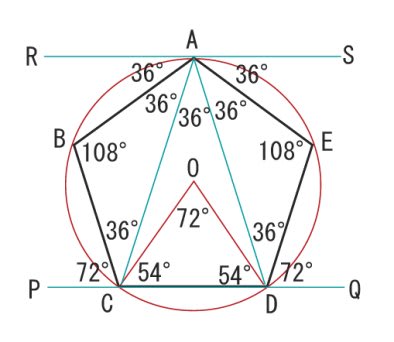
正五角形というだけで 分かる角度は 名寄 算数数学教室より

多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun
中学数学 多角形の内角 外角 中学数学の無料オンライン学習サイトchu Su
6 角形 の 内角 の 和 三角形の内角の和が180 なのはなぜ 小学生に教えるための解説 数学fun
Q Tbn 3aand9gcqqrwa7rlidxkhfciuwqemhonbcknrzmwyhpfcwgetrei0yzg Usqp Cau
Math 多角形の内角の和 働きアリ
中学数学 多角形の内角 外角 中学数学の無料オンライン学習サイトchu Su

小学校5年 算数 正多角形の角の大きさ Youtube
外角
Q Tbn 3aand9gcqw25kbntmryyrmzj1guxvpm4eejo2zffm M Esyayj Mnk Sks Usqp Cau

中学2年生 多角形の内角外角 公式 個別進学教室マナラボ受験 教育情報サイト
小学算数 多角形の内角の和を求める公式 行け 偏差値40プログラマー

多角形の内角と外角 思考力を鍛える数学
算数オリンピックに挑戦 第39回 ライフコラム Nikkei Style
3
正多角形の内角と中心角 家紋の描き方007b 夏貸文庫

この考え方を教えて欲しいです Clear
Q Tbn 3aand9gctm Iwmc58f1ueiedcgzekigxc7jgh40glx85amkbeqj598cc3u Usqp Cau
小5算数 内角の大きさを求めて正多角形を作図しよう ベネッセのプログラミング教育情報
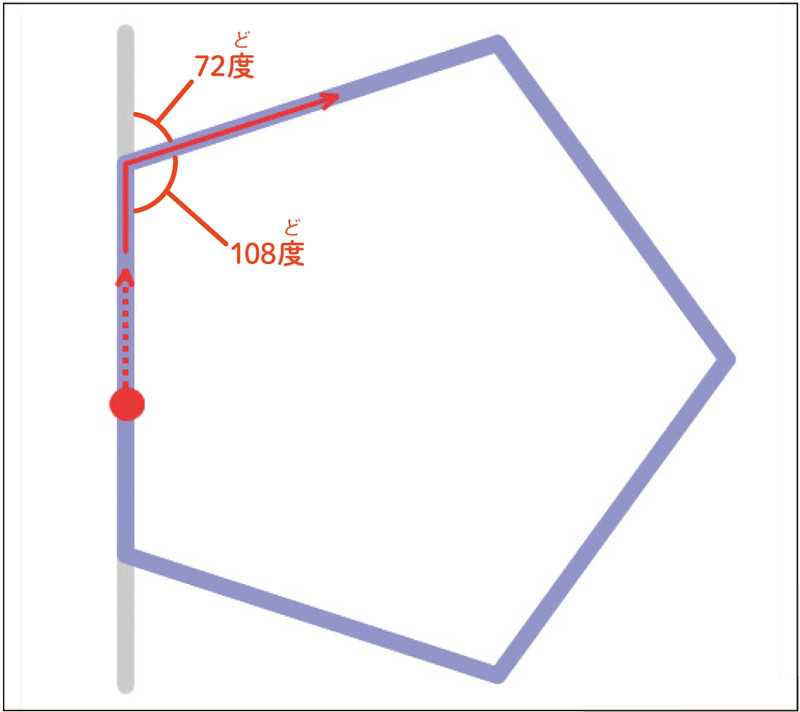
スクラッチ入門 16 正五角形をかいてみよう はじめる 楽しむ プログラミング こどもプログラミング教育のツボ ジャムハウス
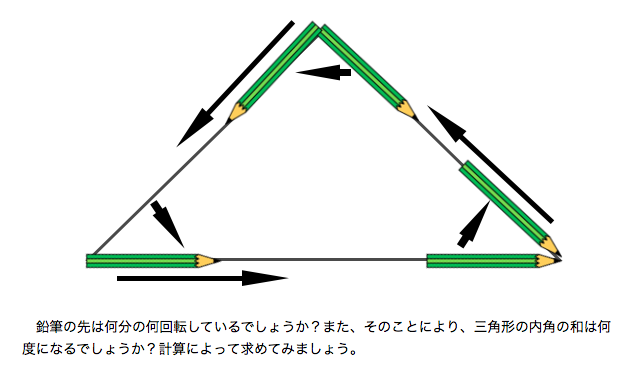
鉛筆コロコロ内角外角 Kojinkai
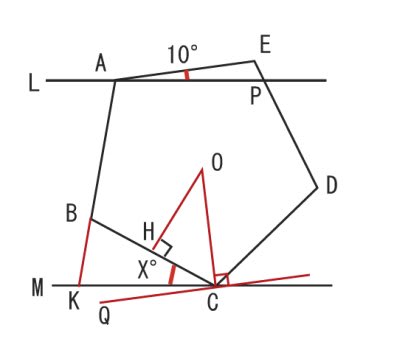
正五角形というだけで 分かる角度は 名寄 算数数学教室より

多角形の内角の和 勉強ナビゲーター
Taphtldk9lbrxm

ペンタゴンの秘密 空間情報クラブ 株式会社インフォマティクス
しょうちゃん 公式ブログ 三角形の内角の和は180度 Powered By Line
正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく

中学数学 三角形と角 五角形の内角 Youtube
Math 多角形の内角の和 働きアリ
南山中学女子部過去問題演習
正五角形を描く ウソの国ー詩と宗教 戸田聡 St5402jp

スクラッチ入門 16 正五角形をかいてみよう はじめる 楽しむ プログラミング こどもプログラミング教育のツボ ジャムハウス
角度 五角形 中学から数学だいすき
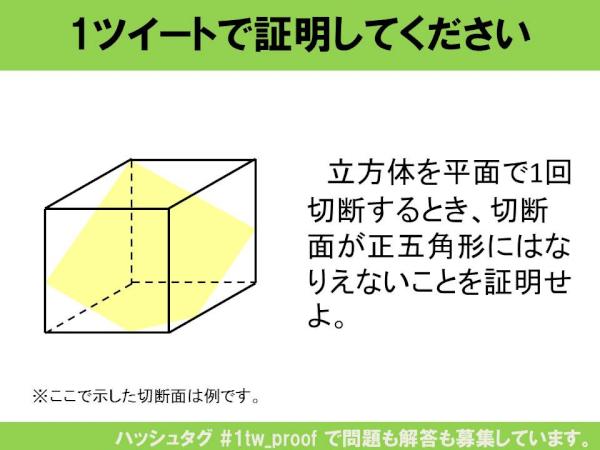
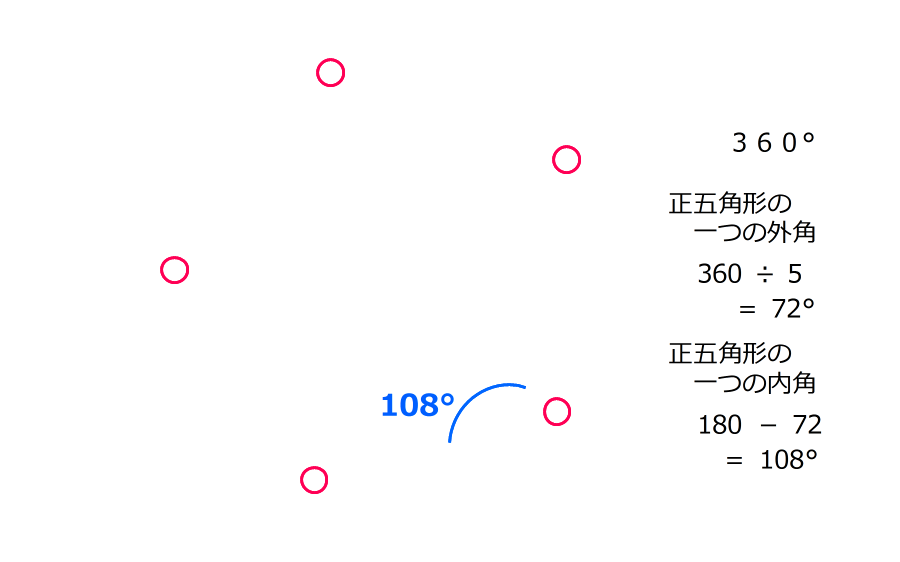
ポット Auf Twitter Tb Lb 正五角形の内角の和は三角形3つ分だから 一つの角は180度 3 5 108度 切断面が五角形 になるためには立方体の頂点を通る平面となる 立方体の頂点を通る平面の Aは 60度 A 90度となる 108度にはならないので 五角形は正五角形には

Murratch 正五角形の内角は108 だから aからbに引いた線のa点の角度は結局18 てことは単純にb a Tan8 a Tan 18 180 P で およそa 0 325 違ってたらスマン 笑
_P1_83J7Rii0_.jpg?1561938029)
五角形の内角の和 ワークシート スクールプレゼンター教材共有サイト スクプレ道場
女子学院中学過去問題演習

多角形の内角の和の公式と外角の和を利用した角度の求め方




