平行四辺形 対角線 長さ ベクトル
平行四辺形であれば、辺 ad と辺 bc は平行で長さが等しいため、ベクトルで書くと\.

平行四辺形 対角線 長さ ベクトル. …凸四辺形では対角線は四辺形の内部にあるが,凹四辺形ではそうとは限らない。2組の対辺がそれぞれ平行である四辺形を平行四辺形といい,頂点がa,b,c,dである平行四辺形を abcdで表す(図3)。 平行四辺形とは,また,2組の対角の大きさがそれぞれ等しい四辺形,2組の対辺の長さがそれぞれ. 解き方がまったくわかりません。この問題です。 平行四辺形abcdにおいて、辺ab、bc、cd、daの中点をそれぞれp、q、r、sとし、対角線ac、bdの交点をoとする。 これら9個の点を始点または終biglobeなんでも相談室は、みんなの「相談(質問)」と「答え(回答)」をつなげ、疑問や悩みを解決できるQ. 12cm C B 11cm.
5 4辺の長さが分かっている四角形の対角線の長さを求める方法 6 四角形pqrsの対象角の長さをa,bとし、この対角線のなす角をoとする 7 四角形abcdは平行四辺形、eは辺ad上の点で、eb=bcである。また. ´ がつくる平行四辺形とa ' とb' がつくる平行四辺形は, 相似比=c :1 の関係にあることがわかる。 したがって, a ' c ´ と b ' c ´ がつくる平行四辺形の対角線の長さも a ' とb' がつくる平行四辺形の対角線の長さのc 倍である。. 新鮮な平行四辺形 対角線 長さ ベクトル ベクトル 平行四辺形証明 位置ベクトルを利用して平行四辺形.
長方形や平行四辺 形を対角線で分割し てできる,2 つの三角 形は合同であること を知り,これらを使っ ていろいろな四角形 る。 それぞれの四角形 の定義や性質の理解 を深め,平行四辺形・ 台形・ひし形をかくこ とができる。. この平行四辺形を「力の平行四辺形」とよび、その対角線が求める合力である。 このようにベクトルは力の方向、大きさを効率よく表してくれる。 矢印の長さは決められておらず 基準となる長さに(力に対して相対関係になる。) 100kgfの力であれば100mmとし. 物理に関する計算問題などでベクトルを作図する場合、「平行四辺形」の図形が現れる。 電験3種のような資格試験の問題では、平行四辺形の種類を手早く判定することが重要である。 何故なら、平行四辺形を「ひし形」「長方形」「正方形」のいずれかに判定することできれば、それらの定義.
16cm 13cm 13 4. 以前の説明 ではベクトル \(\overrightarrow{a}\) と \(\overrightarrow{b}\) が張る平行四辺形に、 そっと \(\| \overrightarrow{a} \times \overrightarrow{b}\|\) と書いていました。. 4 本の辺の長さがすべて等しい平行四辺形をひし形という。 ひし形 \(abcd\) の 2 つの対角線が互いに垂直に交わることを、ベクトルを用いて証明せよ。.
(3)平行四辺形をまず出そう。できるだけ丁寧に、図を描いてみる。 3点あるから、平行四辺形になるのは、どういう点を打てばいいか、割と簡単に見えるよ。 短いほうの対角線の長さ? 図形が二つできそうだけど 短いほうを探せばいいんじゃない?. 定義は「こういう四角形を平行四辺形としよう」と決めたことなので、これを証明することはできません。 「なぜ平行四辺形の向かい合う2組の辺は平行なのか?」と問われたら、 「そのような四角形が平行四辺形と定義されているから」 という答えになってしまいます。. 平行四辺形 abcd と対角線の交点 o.
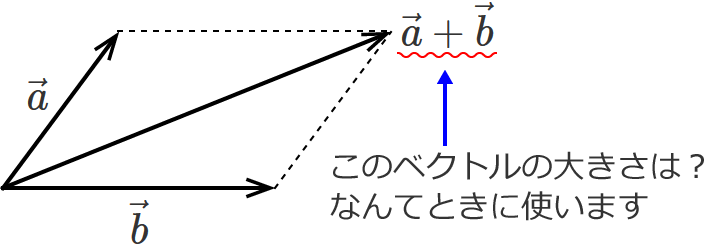
== ベクトルの和 2人の人が,別々の向きに綱を引っ張ると,図のように「合力」は平行四辺形の対角線と一致します.ベクトルの和は,このように「力の合成」のときに,登場します. 2つのベクトルの和を作図するには,. 三角形oabの面積をベクトルを用いて表せたら、平行四辺形oacbの面積も簡単に導出できます。 平行四辺形の対角線を引くと、合同な三角形が 2 つ重なっている形となっています。 ですから、先に求めた、. ここではベクトル積 (クロス積、外積) の大きさは、2 つのベクトルが作る平行四辺形の面積に等しいということについて説明します。.
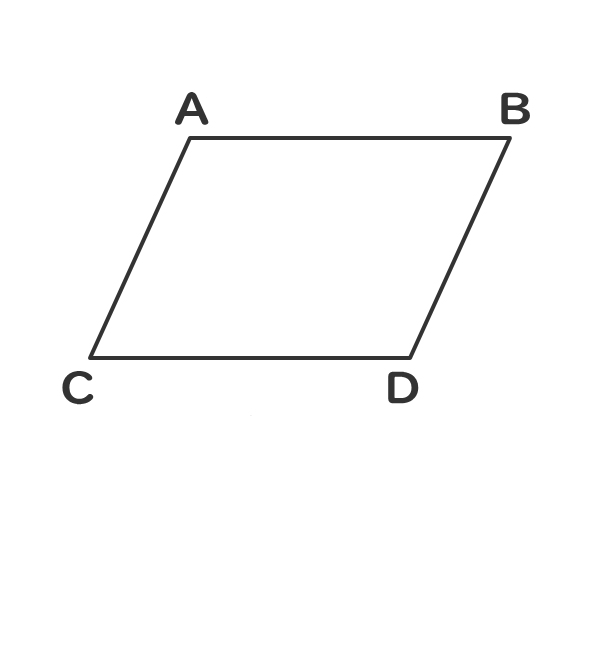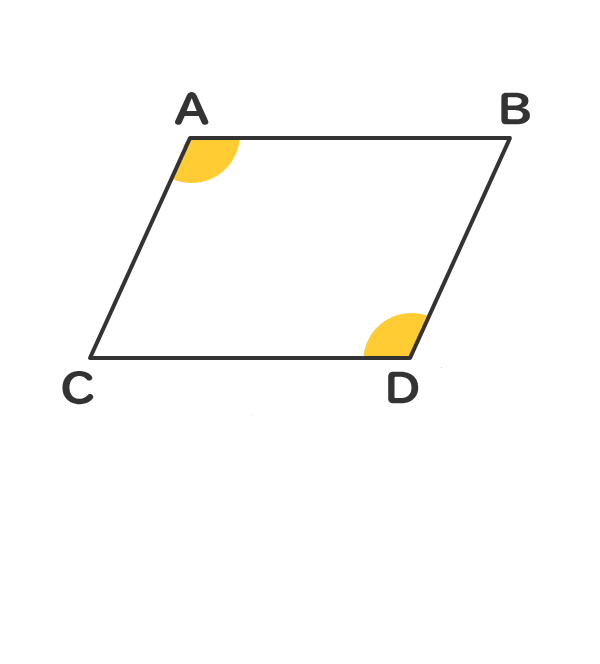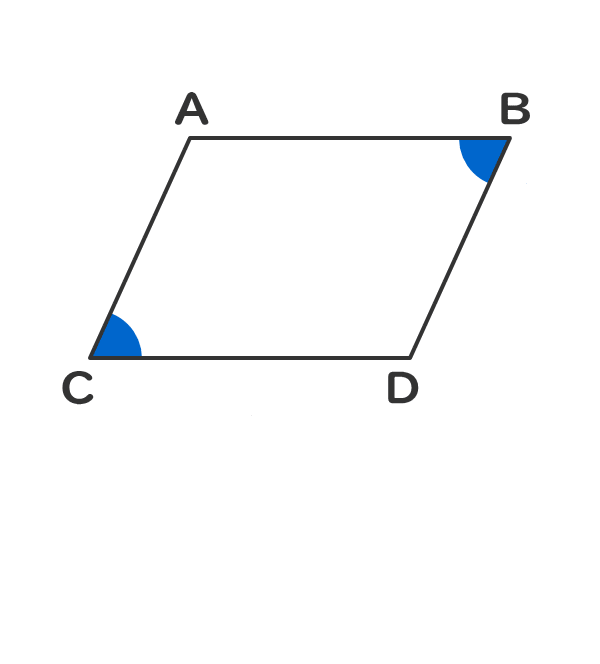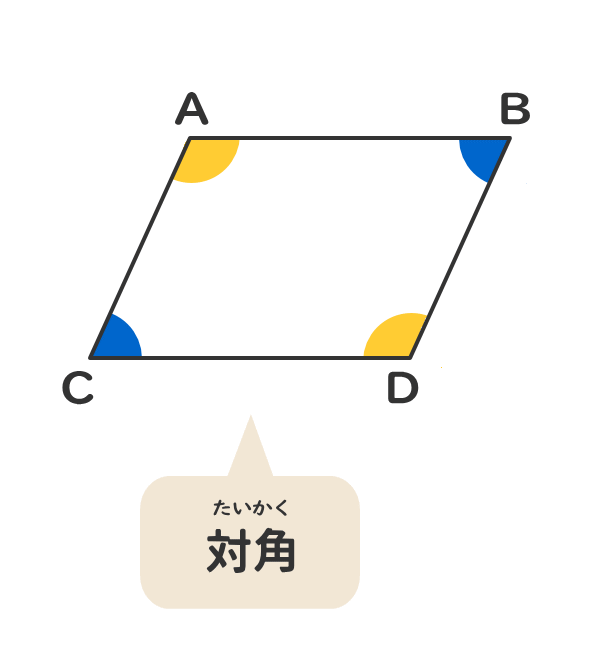
それぞれの中点で交わります。 厳選6パターンの問題に挑戦! それでは、平行四辺形の角度、辺の長さを求める問題をパターン別に解説していきます。 対角、対辺の基本パターン. • ベクトルの和 は,平面のときと同様に(1)「平行四辺形の対角線」または(2)「三角形の2辺の和」の考え方で求めることができる. (1) 2つのベクトルの「始点をそろえて描く」と,平行四辺形の対角線がそれらの和を表す.. 以下の2つのことを、複素数を用いて示せという問題なのですが、どのようにして示せばいいのかわかりません。 どなたか教えてください。 1)平行四辺形の対角線は互いに二等分することを示せ。 2)ひし形の対角線は互いに直交するこ.
平行四辺形の対角線によって、平行四辺形を互いに合同な2つの三角形に分けることができる。 平行四辺形の面積sは 〔底辺〕×〔高さ〕 で求めることができる。これは平行四辺形を面積を変えずに長方形に変形させることで説明できる 。. この記事では「ひし形(菱形)」についての定義や面積の求め方(公式)をできるだけわかりやすく解説していきます。 また、ひし形の計算問題なども紹介していきますので、この記事を通してぜひマスターしてくださいね。 目次ひし形. 上段のように足し合わせる 2つのベクトルの始点が一致しているときは平行四辺形 をつくります。 そして始点からの対角線が2つのベクトルの和になります。.
平行四辺形では、対角線はそれぞれの中点で交わる。 問題に出てくる平行四辺形に対角線が引かれていれば、この性質を利用する可能性がぐっと高まりますね。 それでは、以上の性質を頭に入れた上で証明問題を見ていきましょう。 問題に挑戦!. 向にその目盛りの長さだけ有向線分をひ き,その有向線分の先をa, b, cとする。 次にoa,ob を2辺とする平行四辺形oadb を作り、対角線odをひく。 すると,有向線分odと有向線分ocは方向が同じ(有向線分の向きは逆) で,長さも等しい。それぞれのばねを引く力を有向. 四角形の4つの辺の長さ \(a,b,c,d\) に加え、どちらか一方の対角線の長さ \(e\) が分かっている場合。 四角形を2つの三角形に分けてから各三角形の面積 \(S_1,S_2\) をヘロンの公式を使って求め、それらを合計することで四角形の面積を求めることができます。.
平行四辺形の対角線の求め方を教えてください No.42 下図は、面積が132cmiの平行四辺形ABCDで、AB=13cm、 BC=11 cm、 ZABCは鋭角である。このとき、対角線BDの長さは次のうちどれか。 D A 1. 方べきの定理はセンター試験でも毎年問われるくらい良くでますが、公式を暗記するより覚え方を変えた方法が使えます。 円と関連した問題になりますので、先に円に内接する四角形の対角線が持つ性質を確認しておきましょう。 定理の簡単 …. ・ 二つのベクトルの和は、その二つのベクトルから作られる平行四辺形の対角線となる(ベクトルは平行移動しても変わらないため) ・ 成分表示におけるベクトルの和は、同じ成分どうしを足して求められる ~成分によるベクトルの実数倍~.
Gpo7kr9x9g Lfm

平行四辺形のベクトルの問題です 番の解き方を教えて下さい Clear

考えたけどとても難しかったのでわかる方お願いします 数学 算数のq A 解決済み Okwave
平行四辺形 対角線 長さ ベクトル のギャラリー
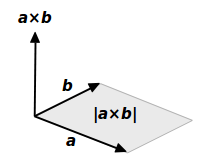
ベクトル積の大きさは平行四辺形の面積 ベクトル解析 基礎からの数学入門
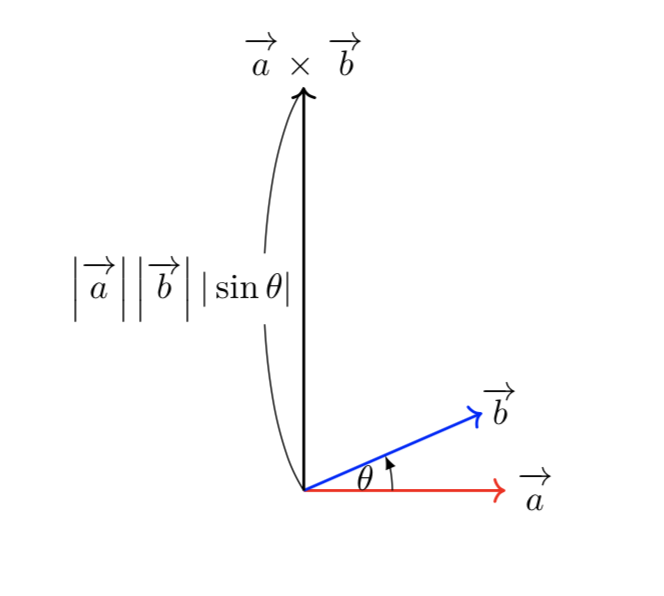
ベクトルの外積の公式やその覚え方とは 高校範囲で役立つ場面についても解説 東大医学部生の相談室

相似 平行四辺形と面積比の問題を徹底解説 数スタ
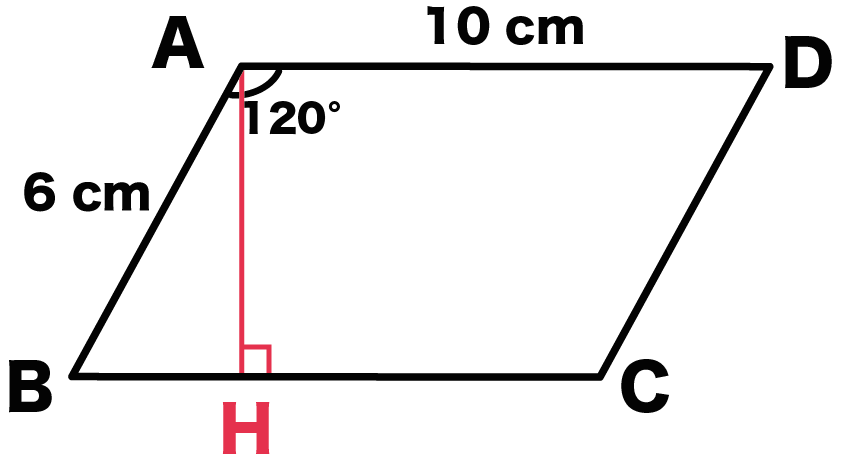
平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
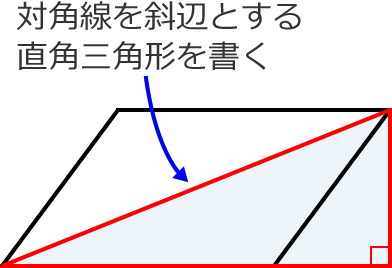
平行四辺形の対角線の長さの求め方

平行四辺形の辺や角を求める Youtube

平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ
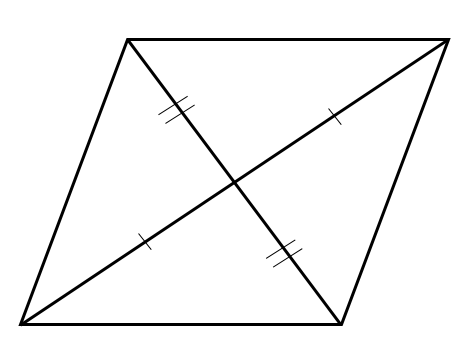
平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ
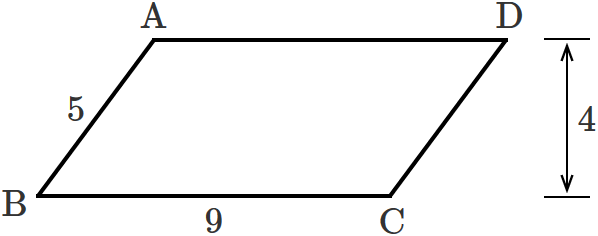
平行四辺形の対角線の長さの求め方
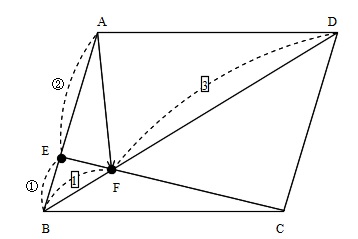
平面ベクトルの内分点外分点の利用と3点が一直線上にある証明

平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく

平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
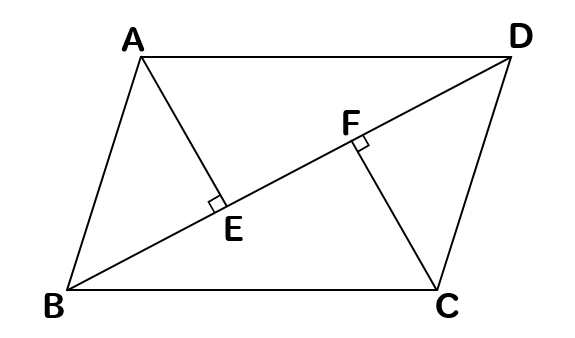
中学数学 平行四辺形の証明問題を徹底解説 数スタ

72 高校数学に関する質問 勉強質問サイト

平行四辺形の定義から性質と条件をわかりやすく証明 特に対角線の性質を抑えよう 遊ぶ数学

ベクトルの和と差 大きさの計算 電験3種ネット

Q Tbn 3aand9gctrj6hxclslip7oahhewkpbjmso4zzh Hu34q Usqp Cau
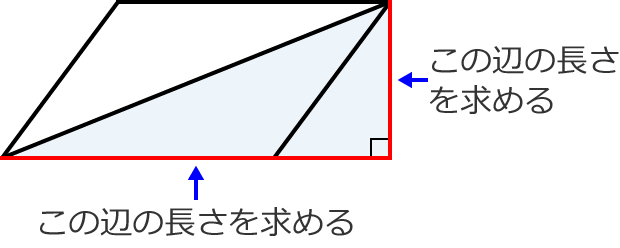
平行四辺形の対角線の長さの求め方

等脚台形の定義と性質 中学校数学の範囲内で考える 身勝手な主張
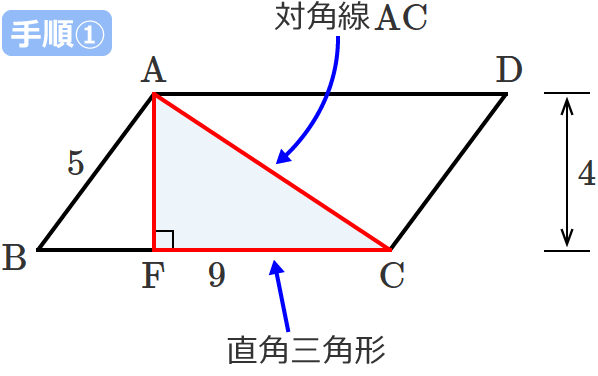
平行四辺形の対角線の長さの求め方
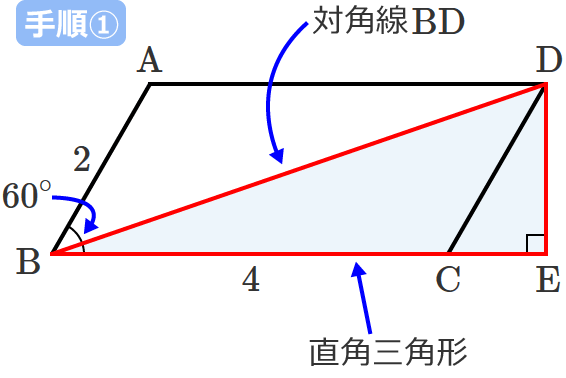
平行四辺形の対角線の長さの求め方

標準 平行四辺形とベクトルの演算 なかけんの数学ノート

いまさら聞けない どうして速度の分解 合成は平行四辺形で考えるのか Koko物理 高校物理
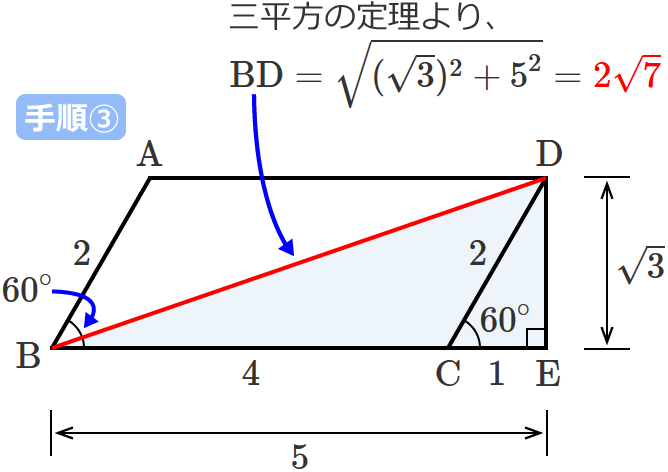
平行四辺形の対角線の長さの求め方

中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット
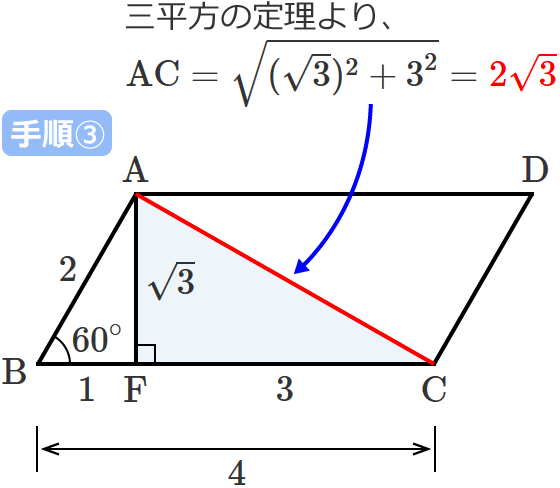
平行四辺形の対角線の長さの求め方

京大13年度第1問を相似だけで解く 数学のカ
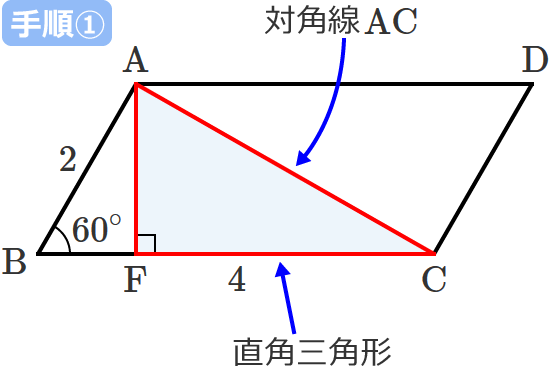
平行四辺形の対角線の長さの求め方
ベクトル平行四辺形証明 位置ベクトルを利用して平行四辺形を Yahoo 知恵袋
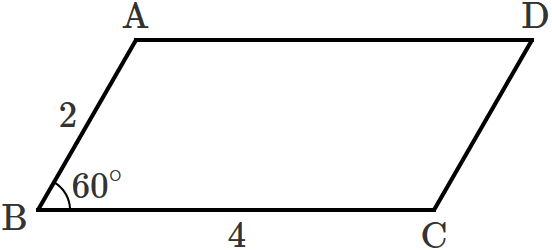
平行四辺形の対角線の長さの求め方

四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun

中点連結定理とは 逆の証明や平行四辺形の問題もわかりやすく解説 遊ぶ数学

この問題ですが なぜabベクトル Dcベクトルでは出来ないんですか Clear
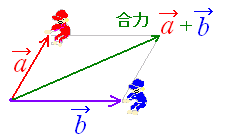
ベクトルの和

高校数学b 角の二等分線のベクトル2パターン 受験の月
証明をする問題です 平行四辺形の対角線は直交していることを証明するのに Yahoo 知恵袋
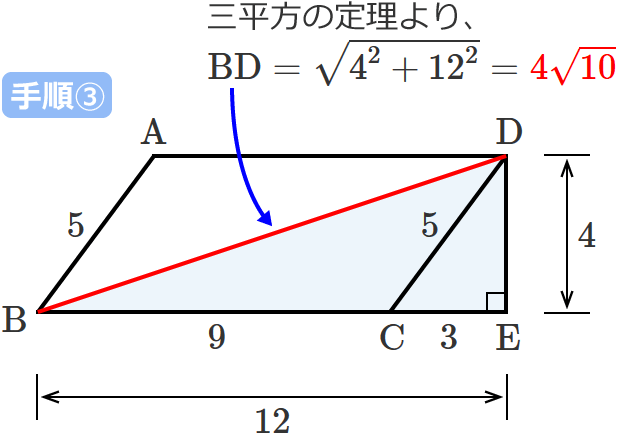
平行四辺形の対角線の長さの求め方
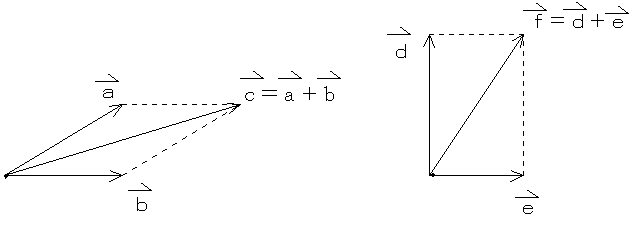
力の平行四辺形

中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット

平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ
勉強しよう数学 中線の長さの公式 中線定理
Gan S Blog フォーラム
Q Tbn 3aand9gcqqrqryxr58uwd7iibvuasirkstewbez Mlpg Usqp Cau
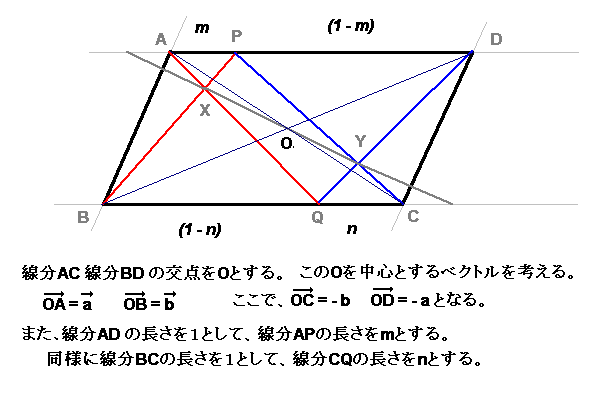
平行四辺形の面積の2等分

平行四辺形の対角線はそれぞれ中点で 高校数学に関する質問 勉強質問サイト
数b 位置ベクトルの問題を教えてください 平行四辺形abcdの Yahoo 知恵袋

ねこ騙し数学

等脚台形の定義と性質 中学校数学の範囲内で考える 身勝手な主張
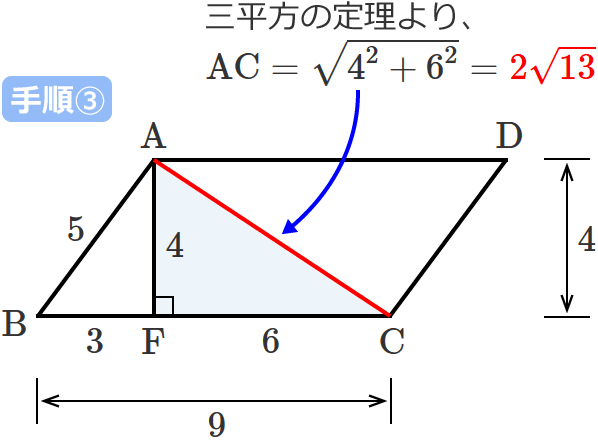
平行四辺形の対角線の長さの求め方
平行四辺形の対角線の長さの求め方

ベクトルの平面図形 高校数学に関する質問 勉強質問サイト

中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット

中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット

ベクトルの和と差 成分表示 高校数学の知識庫
証明をする問題です 平行四辺形の対角線は直交していることを証明するのに Yahoo 知恵袋
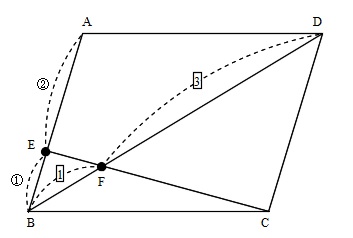
平面ベクトルの内分点外分点の利用と3点が一直線上にある証明

四角形abcdは平行四辺形である 辺bc上にbe Ec 3 2となる 点eを その他 教育 科学 学問 教えて Goo

平行四辺形の対角線の交点を頂点とする三角形の面積 中1の数学の問題 数学 教えて Goo
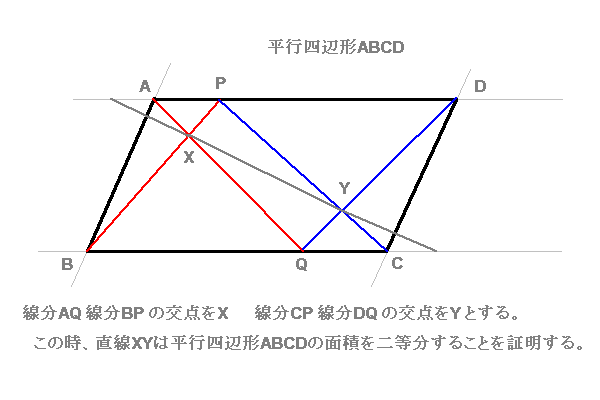
平行四辺形の面積の2等分
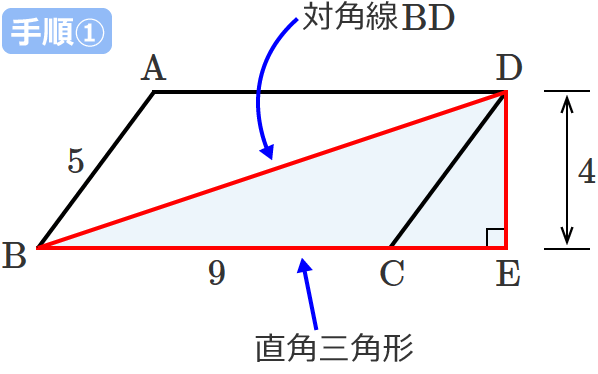
平行四辺形の対角線の長さの求め方

平行四辺形の対角線の求め方を教えてください 高校数学に関する質問 勉強質問サイト
ベクトルの問題です 平行四辺形oacbにおいて 対角線の Yahoo 知恵袋

平行四辺形の問題です 1組の対辺が等しく 1組の対角が等しい四角形 数学 教えて Goo

ベクトルの和と差 大きさの計算 電験3種ネット

標準 平行四辺形と座標 なかけんの数学ノート
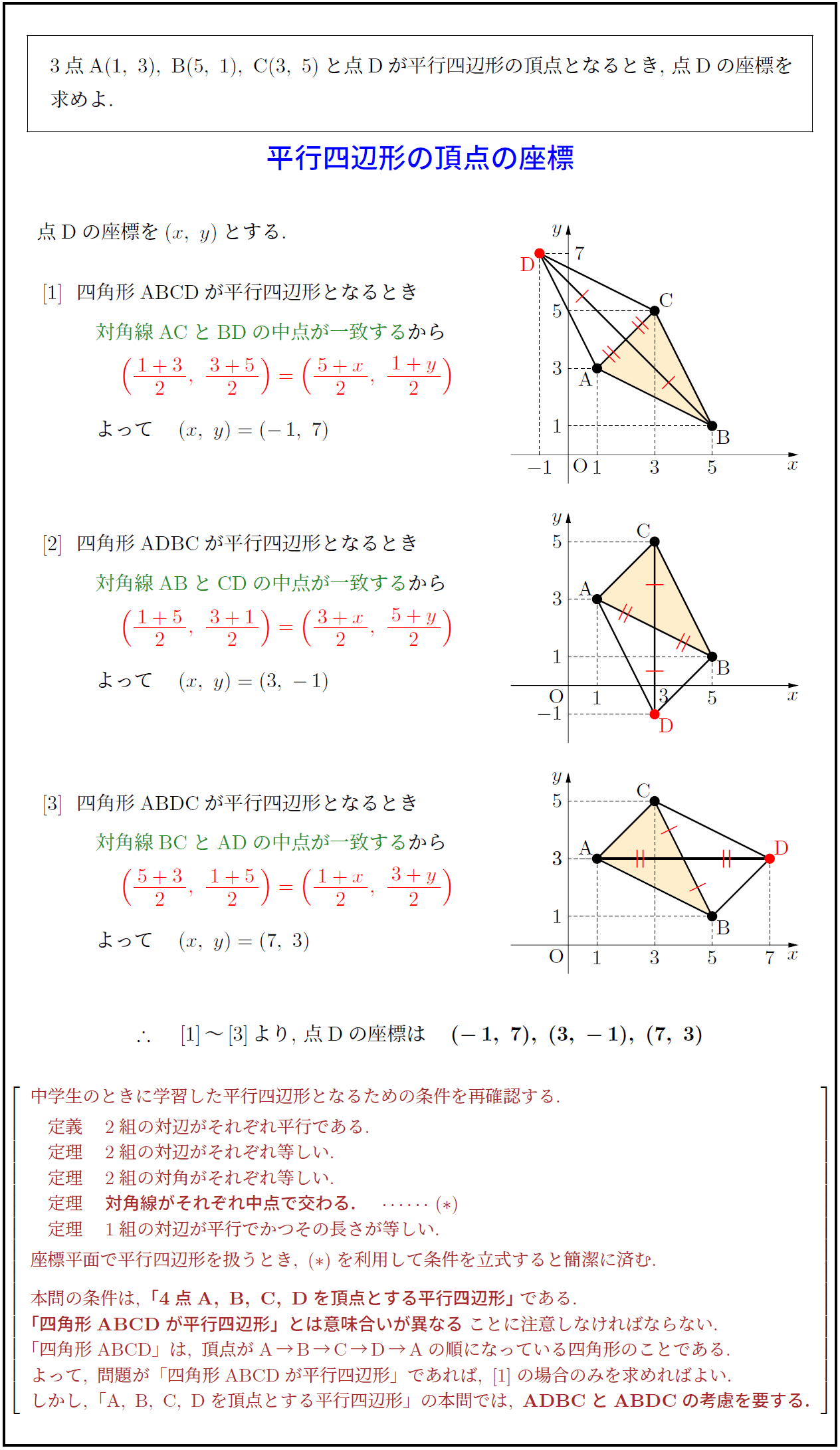
高校数学 平行四辺形の頂点の座標 受験の月

重心 高校数学に関する質問 勉強質問サイト

ベクトルを用いた三角形 平行四辺形の面積の公式と求め方 高校生向け受験応援メディア 受験のミカタ

ベクトルを用いた三角形 平行四辺形の面積の公式と求め方 高校生向け受験応援メディア 受験のミカタ
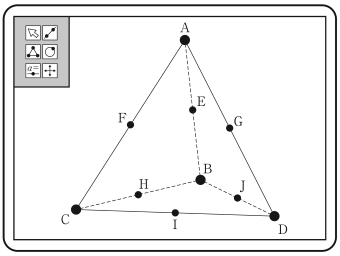
共通テスト試行 H29年度数学ia 問題 正解 解説 ページ 4 Mm参考書

高校数学b 平行六面体と空間ベクトルの演算 受験の月

高校数学b ベクトルの成分表示と平行四辺形 受験の月
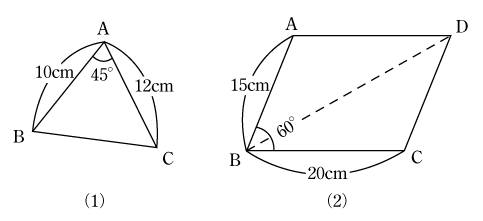
余弦定理と交流ベクトル計算への応用 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会

平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ

関数 グラフ上の平行四辺形の座標 面積 二等分線などの問題を解説 数スタ
平行四辺形対角線の求め方と面積について 対角線acの長さの Yahoo 知恵袋

平行四辺形の対角線の長さの求め方

平行四辺形の対角線の長さの求め方

中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット
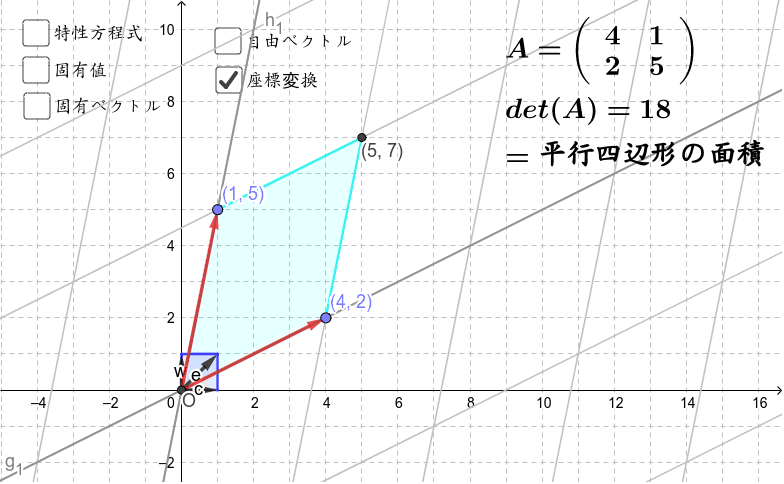
行列 一次変換 Geogebra

ベクトル編 ベクトルで色々な図形を表現する 大学1年生もバッチリ分かる線形代数入門

中学2年 平行四辺形中点の問題 数学 算数のq A 解決済み Okwave

平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ

平行四辺形の問題です 前の続きなのですが 平行四辺形abcd 数学 教えて Goo

四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ

平行四辺形abcdの対角線の交点をoとして 対角線bdにoe ofとなる2 中学校 教えて Goo

ヒント1 ベクトル上に構築された平行四辺形の面積を計算する方法 就学前教育 六月
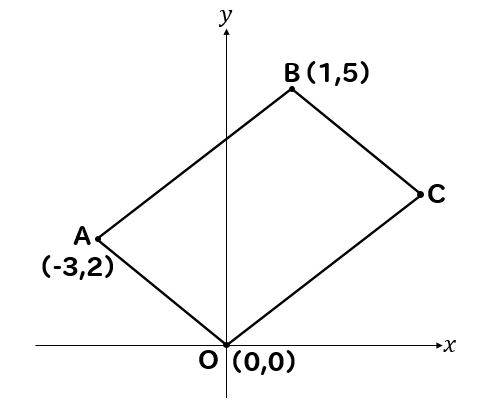
関数 グラフ上の平行四辺形の座標 面積 二等分線などの問題を解説 数スタ

平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく

中学数学 平行四辺形の対角線 面積について 平行四辺形の対角 数学 教えて Goo

数学 高校数学に関する質問 勉強質問サイト

四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
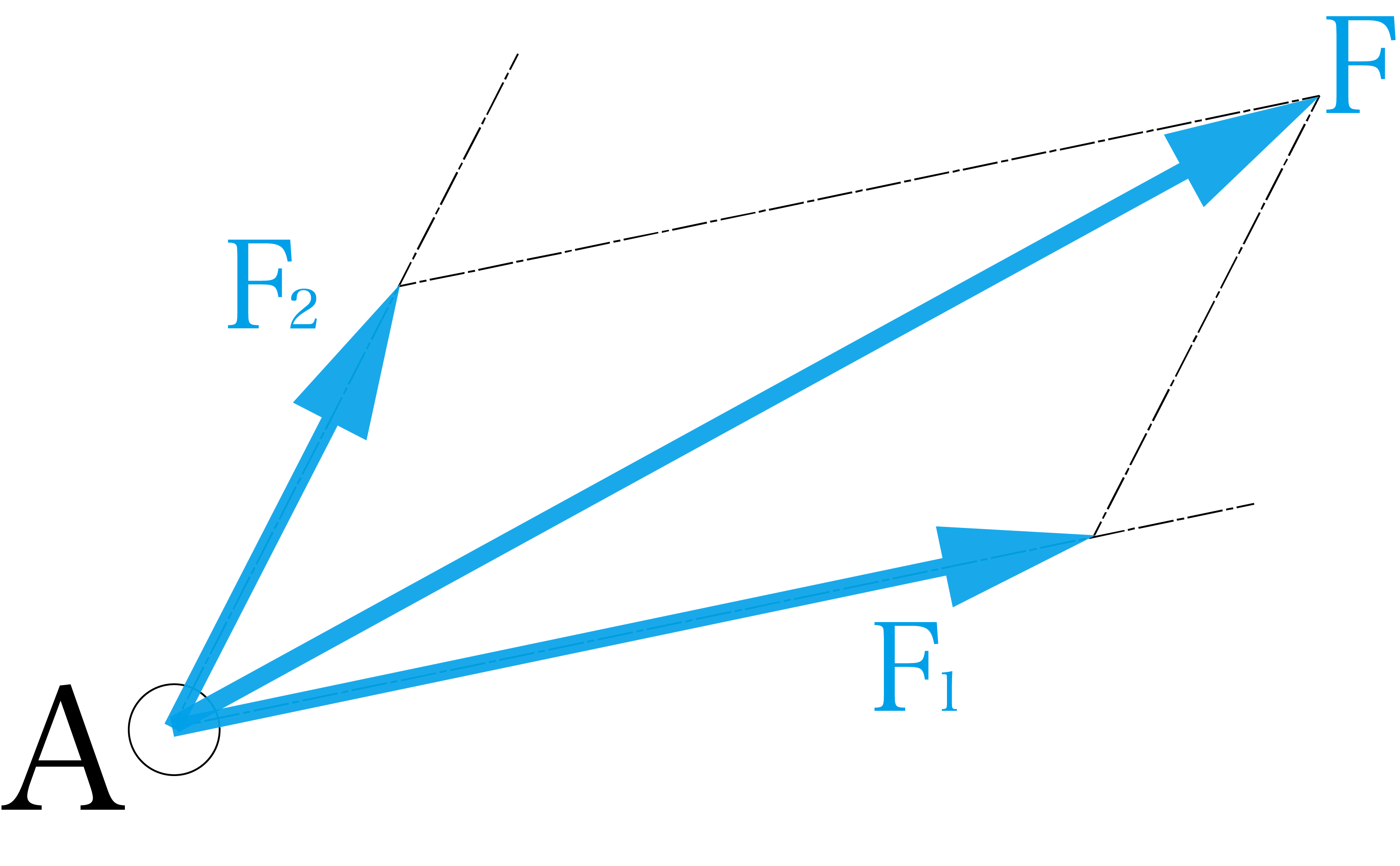
力の作図方法 力の合成と力の分解について 建築学科のための材料力学

中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット

平行四辺形abcdにおいて Abcの重心をg1 Acdの 高校数学に関する質問 勉強質問サイト
平行四辺形の3つの頂点がa 1 1 B 4 2 C 3 7 のとき 第4の頂点 Yahoo 知恵袋

平行四辺形の定義から性質と条件をわかりやすく証明 特に対角線の性質を抑えよう 遊ぶ数学




