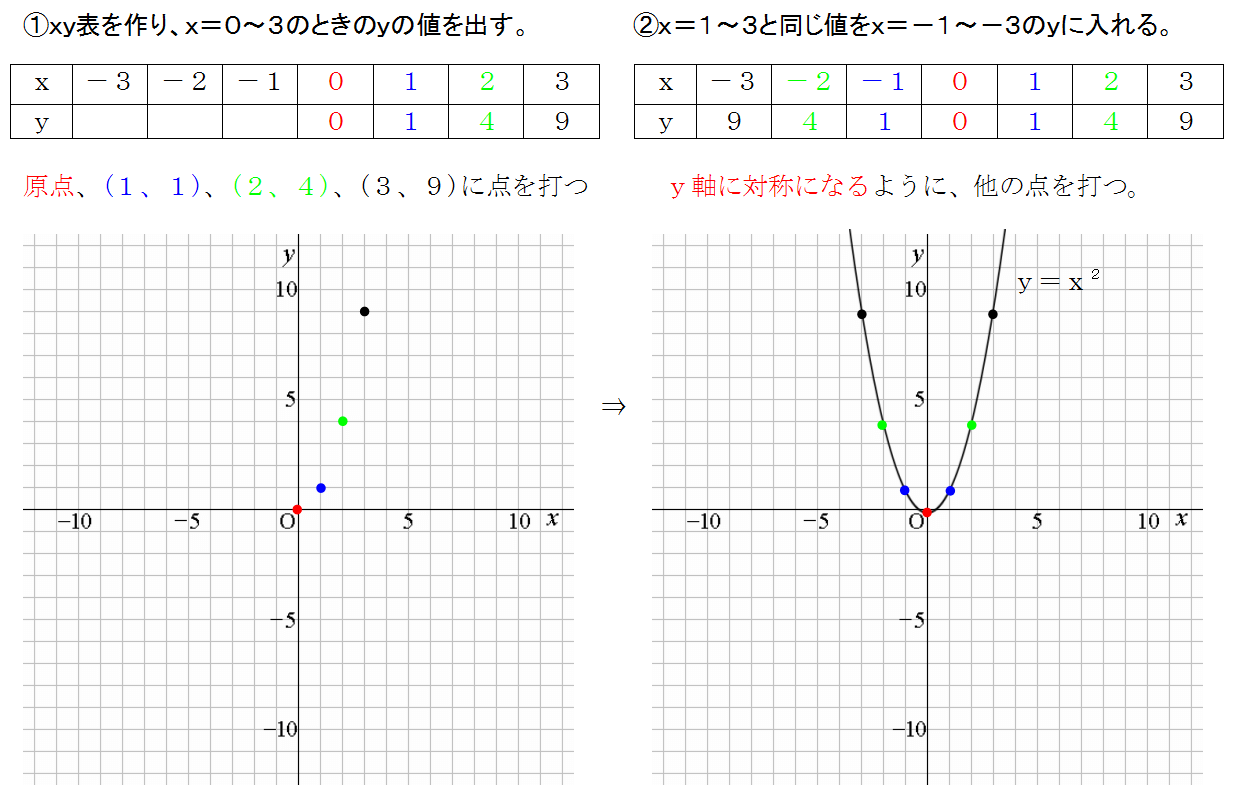
Yax2 グラフ 特徴
・関数y=ax2の特徴(グラフに関する特徴は除く)を、一次関数と比較してまとめる ことができる。(表現・処理) (3) 本時の活動について 前時では、抽出した数量の関係を既習の関数(比例・一次関数)の視点から分類した。.

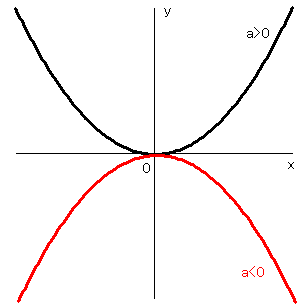
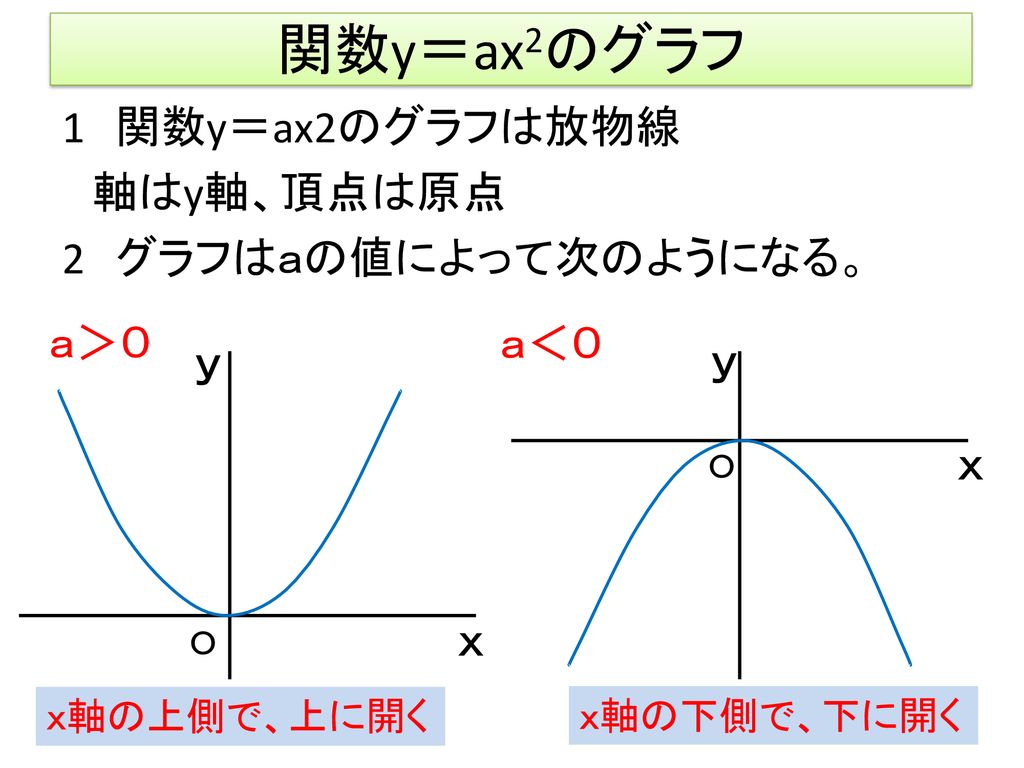
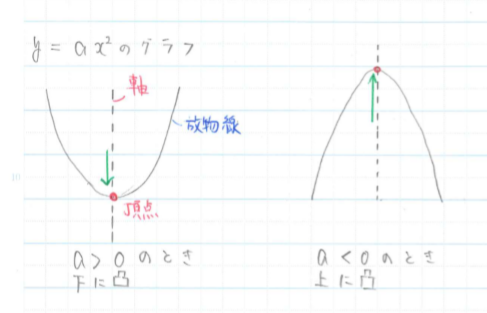
Yax2 グラフ 特徴. ・学習活動:2次関数y = ax2 + q の軸、頂点、グラフ ・指導上の留意点:2次関数 y = ax2 とy = ax2 + q のグラフをかき、平行移動及びグラフの特徴を理解させる。2次関数 y = ax2 + qの軸の方程式、頂点の座標を求めさせる。 ・評価(観点、方法等):y =. 定期テストで、試験範囲になっていれば、100%出題されるところです。しっかりおさえていきましょう。2次関数のグラフの特徴 原点を通る(頂点は、原点である) y軸に対称 放物線になる a>0のとき、上に開く。a<0のとき、下に開く。. 無視する! これがポイントですね(^^) y=ax2乗のグラフ書き方 まとめ.
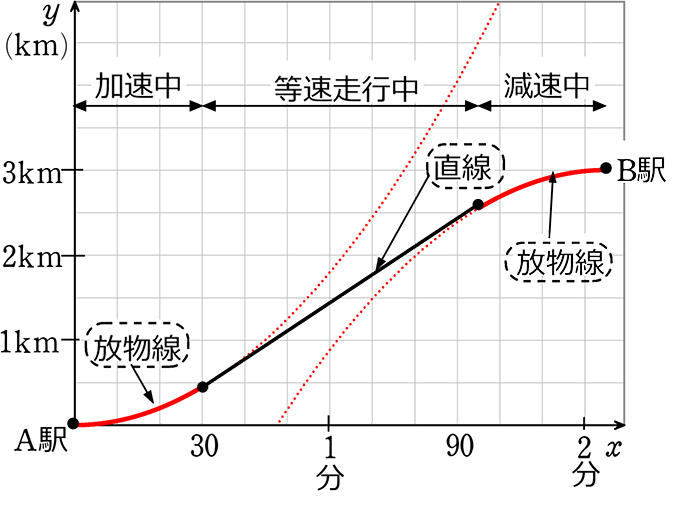
グラフ(1) Aプランのグ ラフの切片は 基本料金 ・一次関数のグラフは直線 になることを知り、一次 関数のグラフと比例の グラフの関係を理解す る。 一次関数のグ ラフの特徴を 比例のグラフ と比較して考 察することが できる。(ア、 ウ、エ) 一次関数のグ. 式,グラフを関連 式,グラフを用いて,を相互に関連付けるで表現したり,表,変化の割合など,関 ( 付けて理解する。本その特徴を調べようなどして見いだすこ式,グラフから,そ数y=ax2 の特徴を理 時としている。 とができる。. ここでは、放物線を図形的な観点から見ていくことにします。 放物線の定義 基本円の方程式で見たように、円の方程式は次のように表されます。 (x-a)^2+(y-b)^2=r^2 このグラフは、点 $(a,b)$.
関数y=ax2のグラフとその特徴 関数y=ax2のグラフとaの値との関係 ☆方眼のないグラフで、y=ax2のaの値の違いから式とグラフの対応を判断し、説明する活動を通して関数y=ax2のグラフの理解を深める。- 小学生・中学生が勉強するならスクールTV。. 本時の学習内容「関数 y = a x 2 ( a >0)をグラフに表し、その特徴を調べよう」を知る。. 中3数学 ゆうき先生.
Y=ax2 を取り扱い、変化の割合やグラフの特徴など関数の理解を一層深めていくことになる。 既習事項の比例や1次関数のグラフが直線になるのと異なり、グラフが曲線になることから、 理解が困難な部分もあるため、十分な配慮が必要であると考える。. 2乗に比例する関数のグラフの特徴の問題です基本のポイント 必ず原点を通り、その原点が頂点である y軸について対称である a > 0のときは上に開き、a < 0のときは下に開く aの絶対値が小さいほどグラフの開きが大きい y=ax2のグラフとy=-ax2のグラフはx軸について対象である。. ァ y=ax2 ぉょび y=ax2+bのグラフ。(数係数の場合。) イ 「ア」のグラフの特徴および係数と形との関係。 ウ 「ア」に掲げる二次関数と一次関数との値の変化のしかたの違い。 工 「ア」のグラフを用いた二次方程式の解法。 また、文部省指導書.
中学数学 \(y=ax^2\) のグラフ 中学数学 \(y=ax^2\) のグラフを読み取る 中学数学 \(y=ax^2\)と変域 中学数学 \(y=ax^2\) 変化の割合の意味 中学数学変化の割合・必殺の公式 中学数学平均の速さ 中学数学制動距離. 放物線、軸、頂点、関数y=ax 2 のグラフのかき方と特徴. 二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の.
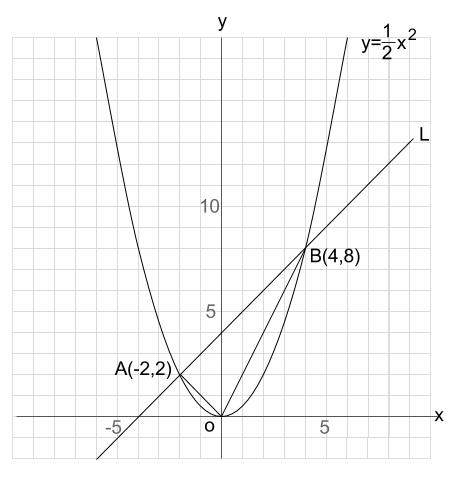
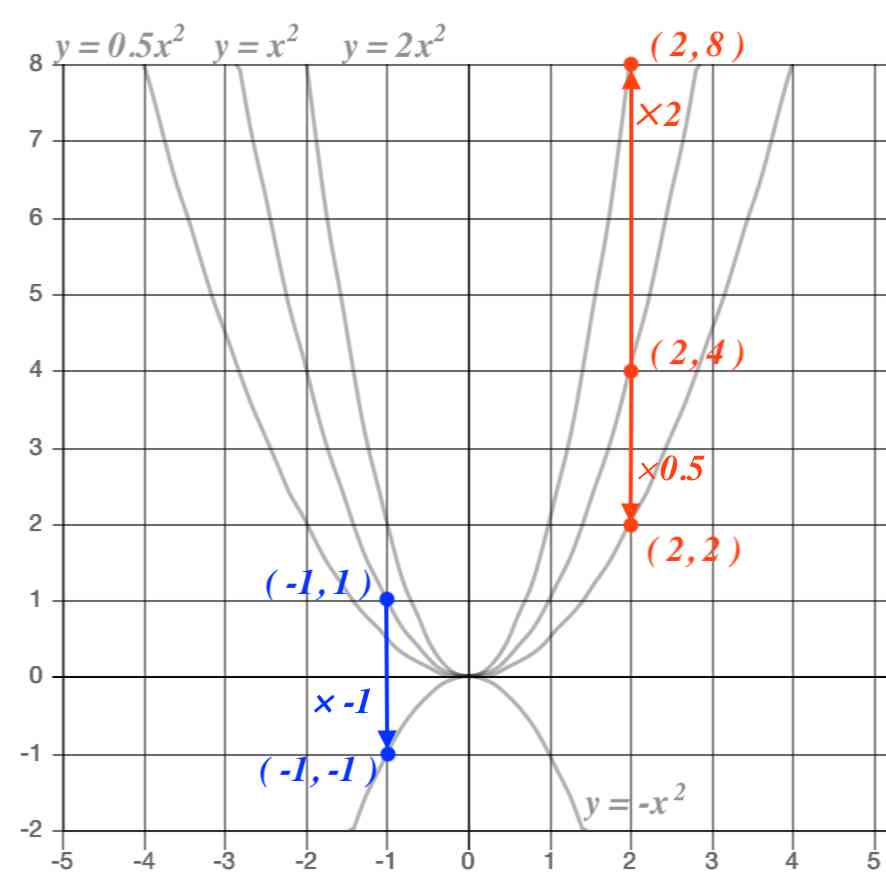
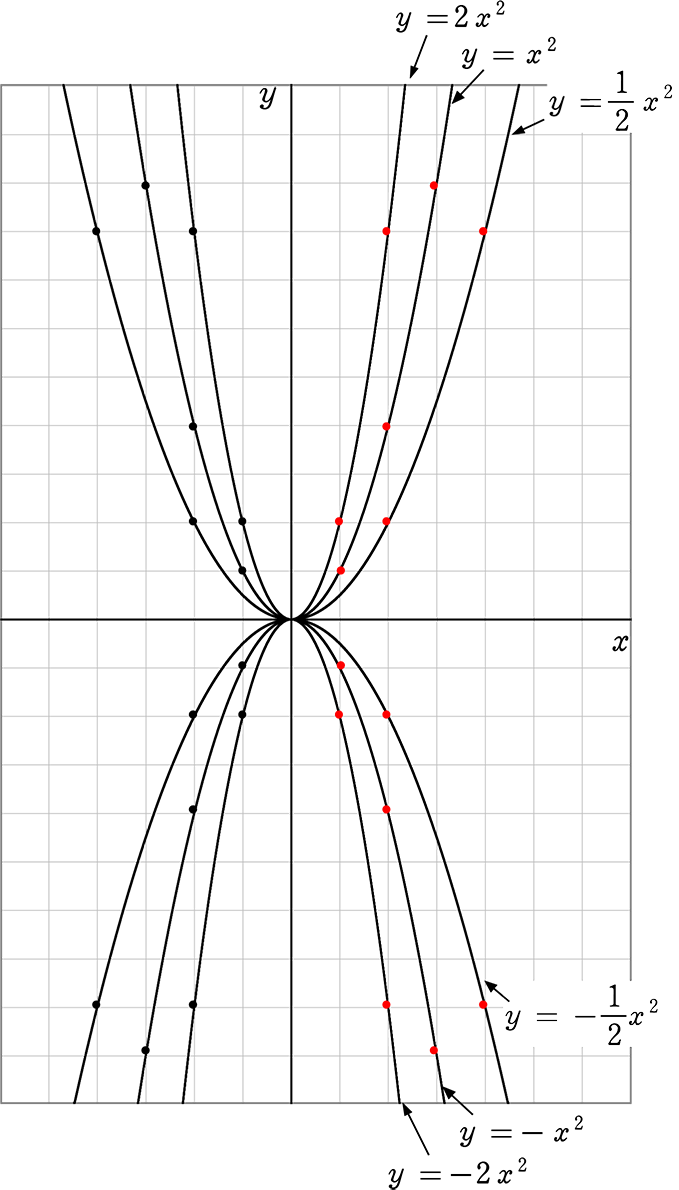
A(2,1), B(2,8) A(4, -4), B(4, -8) A(-3, 1), (-3, -9) 図の放物線lはy= 1 2 x 2 の グラフで、放物線mはy=ax 2 のグラフである。lとmがx軸に平行な直線nと交わる点をそれぞれA, Bとする。Aのx座標が4. <関数y=ax2 のグラフの特徴> <グラフの開き> ・線対称、線対称、x軸の上側にあるということ を記載 y=2x2 のグラフとy=x2 のグラフを比べる →y=1 2 x2 のグラフ →y=ax2 で、a<0のときのグラフ(y=-x2 のグラフ) ・y=-x2 のグラフ → y=-2x2、y=- 1 2. れを式で表現する。また,グラフの特徴から関数関係を見いだし,式で表現する。このようにして 表,式,グラフを単独で用いるのではなく相互に関連付けて関数の特徴を調べ,関数y=ax2 につ いて多面的に考察させ,深く考える力を高めたい。.
Http Www Edu City Fukuyama Hiroshima Jp Chu Johoku Revolution Actionplan Syutaiteki Manabi01 6 Shidouan K29 07m Pdf 無視. ・関数y=x2のグラフに関心をもち,その特徴を調べよ うとする。 ・関数y=x2について,表,グラフを表現することがで きる。 行動・発言 ノート ワークシート ・関数y=ax2(2) y=ax2のグラ フをかいて,それ らのグラフを考 察する。. 4 ・関数y=aχ2 のグラフ のかき方とその特徴を理解 する。 ・関数y=aχ2 のグラフをかくことができる。 ・関数のグラフの特徴を、比例定数の符号や絶対値 と関連付けて理解している。 (行動・発言・ノート・ワークシート).
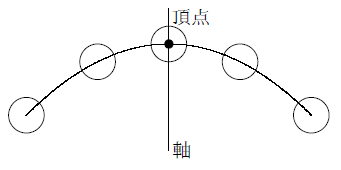
Y=ax 2 のグラフで,軸と放物線が交わるところ(原点)を頂点といいます. (三角形や四角形と異なり,角(かど)がなくても頂点といいます.参考までに,高等学校で習う楕円(だえん)では次のように頂点が4個あります.) y=ax 2 のグラフは,どんなaの値に対しても,頂点は原点になり. ・y=ax2 のグラフの 特徴を見つけ,a の値との関係を 考える。 関数y=ax2 のグ ラフの特徴を調 べ,グラフをかこ うとしている。 a の値の変化と グラフの形を関 連付けて調べ, グラフの特徴を 放物線や軸,頂 点の意味と関数 y=ax2 のグラフ の特徴を理解し. ・関数y = ax2 について、表、式、グラフを相互に関連付けて理解すること。 ・関数y = ax 2 を用いて具体的な事象をとらえ説明すること。 ・いろいろな事象の中に、関数関係があることを理解すること。.
このページでは、二次関数のグラフを決定するのに必要な要素や、グラフの特徴について解説します。 ある二次関数のグラフを言葉だけで説明するとき、最もわかりやすいのは、 グラフの形と位置 について説明することだと思います。. ・関数y=ax2 2の式を求めることができる。 ・関数y=x のグラフの特徴をxの値を 0.1 お きに点をとることを通して考察する。 ・関数y=x2のグラフは滑らかな曲線になるこ とがわかる。 ・関数y=ax2のグラフをかくことができる。. 与えられた条件からy=ax2の式を求めること 2 関数y=ax2のグラフ C(1)イ 関数y=ax2のグラフとその特徴.
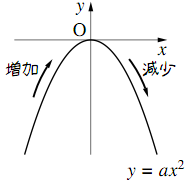
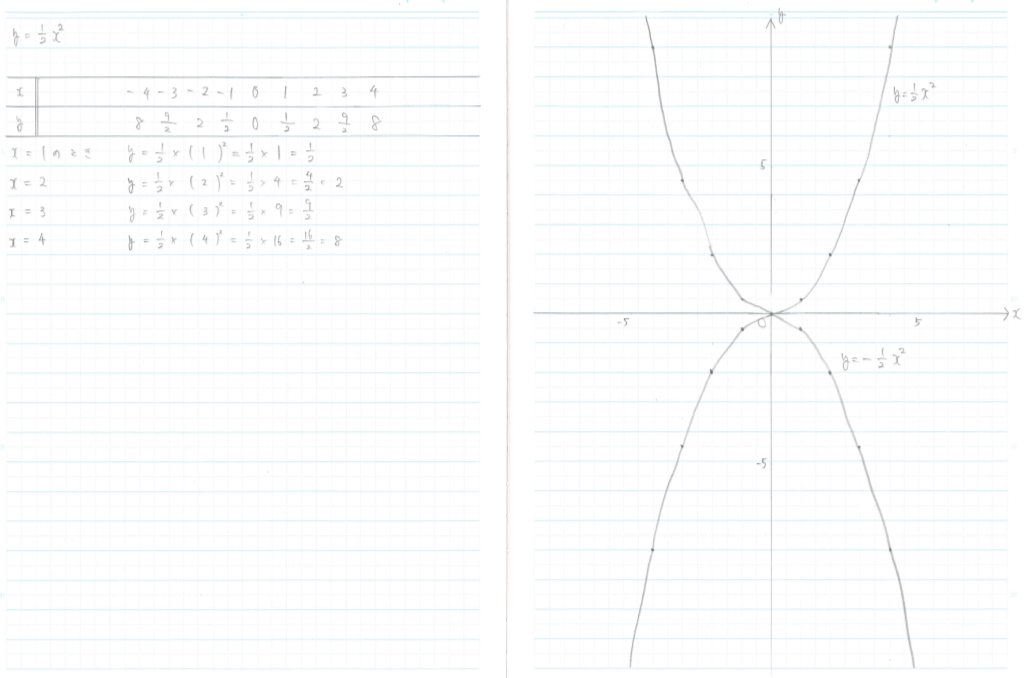
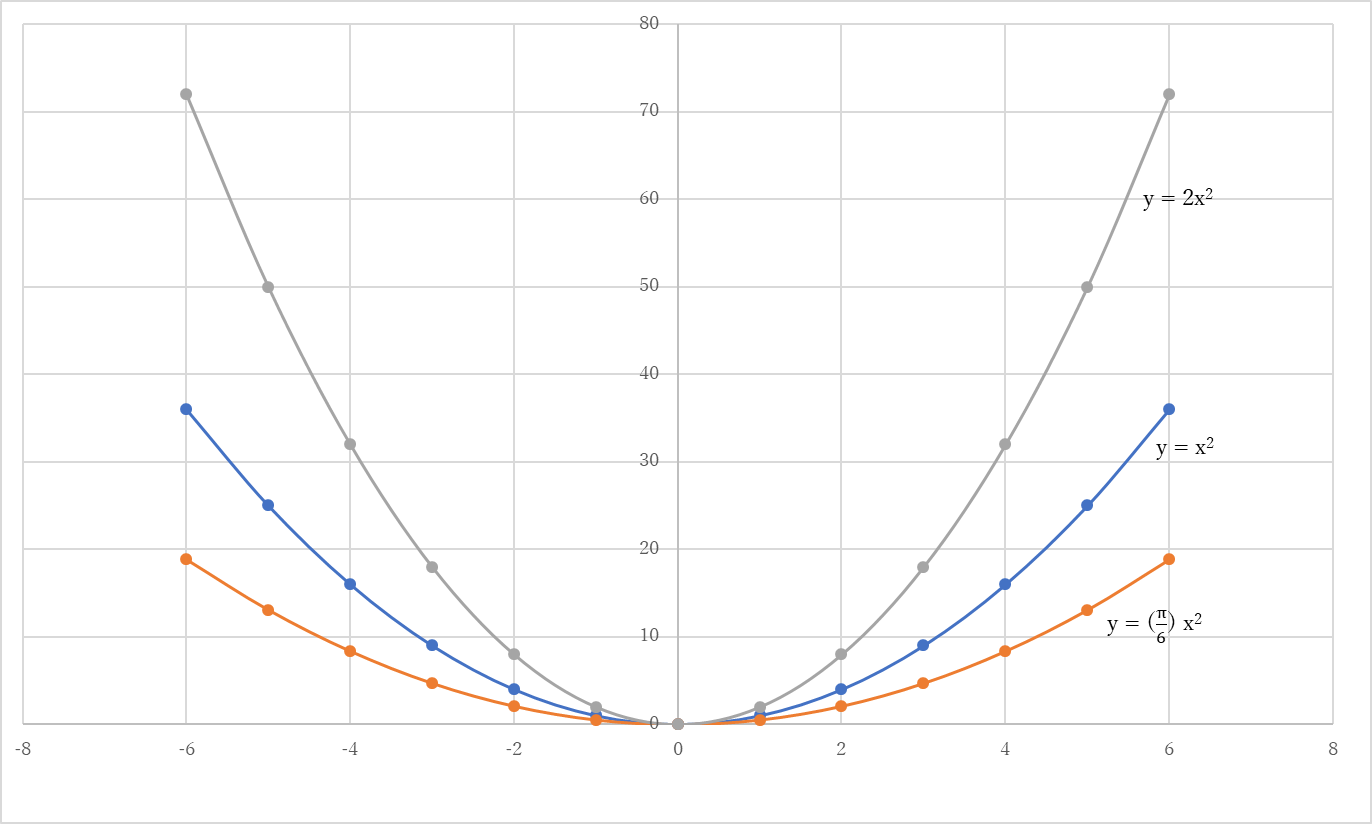
VMA-03 2 2 乗に比例する関数のグラフ ここでは,関数y=ax2 のグラフとその特徴について学習してみましょう。 関数y=ax2 において,x=k,-kのときのyの値をそれぞれ求 めると,ともに y=ak2, ya k ak=-=_i2 2 となるから, y=ax2 のグラフは 軸に関して対称であるといえます。. 左のグラフを見て,3つの特徴があることが分かります。グラフを見て考えてください。 特徴1 a>0 のとき,放物線は上に開いている。 このとき,下に凸(とつ)と呼ぶ。 a<0 のとき,放物線は下に開いている。 このとき,上に凸(とつ)と呼ぶ。 特徴2. 中3数学。2乗に比例する関数 (y = ax²)。この a は「変化の割合」? xの値が「0から2まで」増加する? 分からん…(ガクッ)倒れ込む中学生。立て、立つんだトォォォォ~ッ! オール5家庭教師、見参ッ! 2次関数のコツ、成績アップ法を公開。.
式、値の変化、グラフなどから関数関係を分析し、その特徴を理解し、問題を関数的に解決する y =ax2 y = a x 2 の関係にある数量を、表、式で表したり、変数の変域、変化の割合を求めたり、曲線上の2点を通る直線の式を求めることができる. ・関数y=ax2のグラフの特徴をまとめる。 用語・記号放物線 関数y=ax2のグラフについて,aの値と関連づけて,その特徴を考えることができる。 関数y=ax2のグラフの特徴を理解している。 3 関数y=ax2の値の変化 (教科書p.102~107) 6 関数y=ax2の値の変化. 前時のまとめを基に、関数 y = x 2 のグラフの特徴を思い出す。 :.
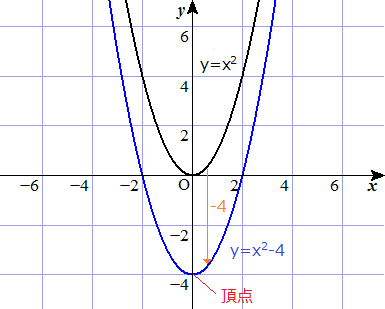
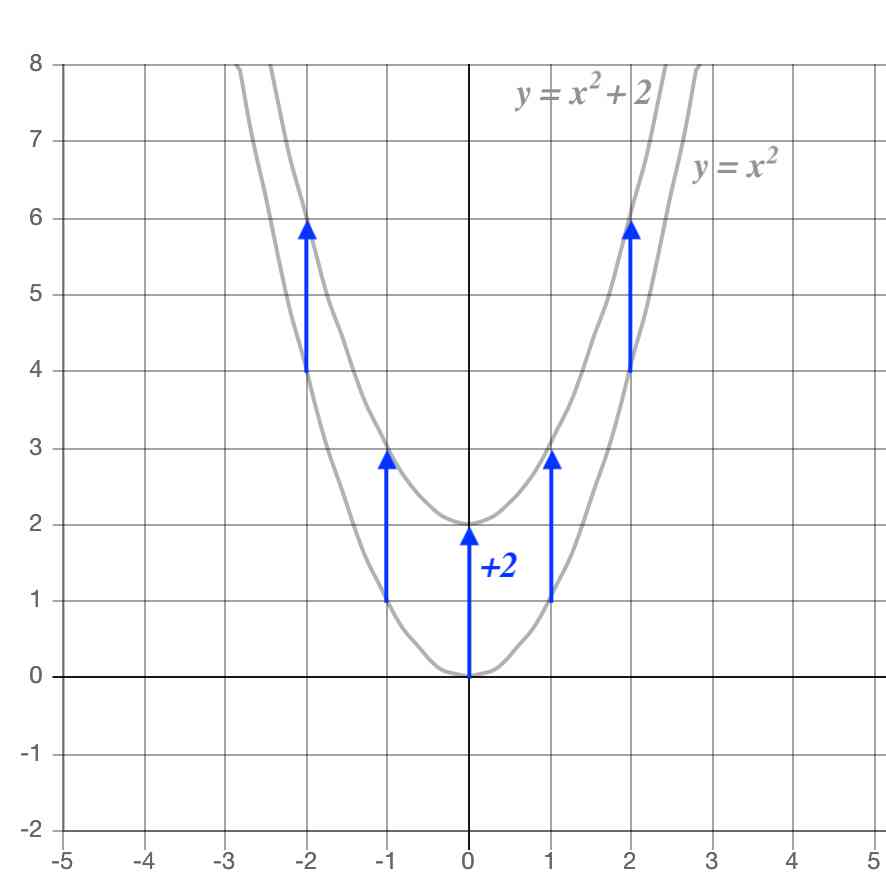
ねらい「関数y=ax2のグラフをかき、その特徴を理解する。」 ↓ y=x2のグラフをかき、特徴を調べる。 ↓ y=2x2 、y=12x2のグラフをかく。 ↓ y=ーx2のグラフをかき、特徴を調べる。 ↓. なる関数やグラフ が階段状になる関 数について、対応 する値を求め、表 やグラフで表すこ とができる。 関数y=ax2のグラ フについて、aの 値の変化とグラフ の形を関連づけて 調べ、特徴を考え ることができる。 具体的な事象につ いて、関数y=ax2. 2次関数の教科書の指導の流れは、①y=ax2のグラフの特徴とaの意味(中学の復習から放物線の特 徴まで)②y=ax2+qのグラフとqの意味(y方向への平行移動)③y = a(x- p)2のグラフとpの意 味(x方向への平行移動)④y = a(x一p)2+qのグラフとP,qの意味(x、y方向への平行移動)⑤.
中3数学関数y=ax2乗のグラフの問題の解き方を教えてください。 ----- 問題 下の図は、関数y=ax2乗、y=4xのグラフで、点Aはグラフの交点である。 ABがx軸と平行になるようにy軸上に点Bをとり、また、BCがAOと平行となるようにx軸上に点Cをとる。. のグラフ (1) 関数y=ax2 のグラフの 特徴を、a>0のときの a の値に着目して調べ る。 関数y=ax2 (a>0)のグ ラフをかくこ とができる。 (学習活動の観 察、ノートの分 析) y=ax2 のa>0 のときのa の 値とグラフの 関係を理解し ている。(学習 活動の観察、発.

二次関数y ax 2 のグラフは点a 4 2 を通っている y線 数学 教えて Goo
二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師

中学数学 二次関数y Ax2のグラフから式を3秒で読み取る方法 Qikeru 学びを楽しくわかりやすく
Yax2 グラフ 特徴 のギャラリー

中学3年 関数 Y Ax2乗 利用 Clear
y ax 2のグラフ2

2次関数のグラフと直線
2

2次関数のグラフ
栃木県総合教育センター 算数 数学 学びの杜 中学校3年生 数学 関数y ax 2のグラフ
2

中3数学 2次関数のグラフの特徴と練習問題
Y Ax 2のグラフ 数学i フリー教材開発コミュニティ Ftext
例題で学ぶ高校数学 Y Ax2 Q
2

Y Ax2乗の利用 放物線と直線による面積 中学3年の問題をイチから解説 中学数学 理科の学習まとめサイト

例題で学ぶ高校数学 Y Ax2

微分とは何か 中学生でも分かる微分のイメージ

二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ
中学数学 Y Ax 2 図形との融合問題 中学数学の無料オンライン学習サイトchu Su

基礎数学 3回目

2次関数とグラフ 勉強動画ラボ 高校数学を中心とした無料の学習動画まとめ
Q Tbn 3aand9gcqsxyjiqhnwwxifkkmsowbwqrpn6syl2fyikhtdq0a7ebfva0 Usqp Cau

二次関数y Ax2の放物線にみられる5つの特徴 Qikeru 学びを楽しくわかりやすく

一般形のグラフの特徴
二次関数y Ax2の放物線にみられる5つの特徴 Qikeru 学びを楽しくわかりやすく

関数y Ax2乗の変域の求め方 勉強ナビゲーター
二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師

中3数学 Y Ax 2のグラフ A 0 映像授業のtry It トライイット
Y 2x 2のグラフ Takapの数学日記
中学数学 関数
ねらい 関数y ax2のグラフをかき その特徴を理解する Ppt Download

Y Ax 2 Bx Cのグラフ 数学i フリー教材開発コミュニティ Ftext
Tossランド 関数の初期の指導 Y Ax2 その2

中学生がつまずきやすい数学分野
放物線のグラフ 中学勉強 おやじさん ネット

中学数学 二次関数y Ax2のグラフから式を3秒で読み取る方法 Qikeru 学びを楽しくわかりやすく

Y Ax 2

中学数学 1次関数と2次関数y Ax2のグラフの3つの違い Qikeru 学びを楽しくわかりやすく
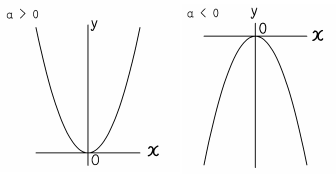
2乗に比例する関数 グラフ

原点を通る2次関数のグラフ
Y Ax のグラフ 中学3年 数学クラブ

2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ

中学数学 二次関数y Ax2のグラフの書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

例題で学ぶ高校数学 Y Ax2

2次関数とグラフ 勉強動画ラボ 高校数学を中心とした無料の学習動画まとめ
2

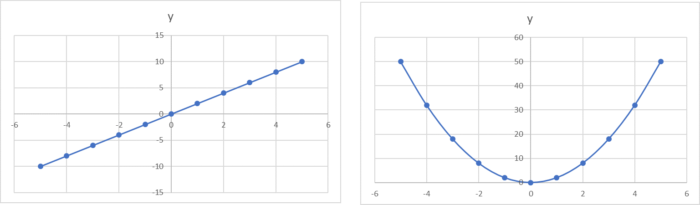
Y Ax 2のグラフをexcelで作成したい Y Ax 2のグラフをexcelで作成し Excel エクセル 教えて Goo
Q Tbn 3aand9gcssq6vpskngjoqennuuhrn Ocyr Xow1rbdho0qypdq9bmqvetp Usqp Cau
二次関数のグラフの書き方
Tossランド 関数の初期の指導 Y Ax2 その2
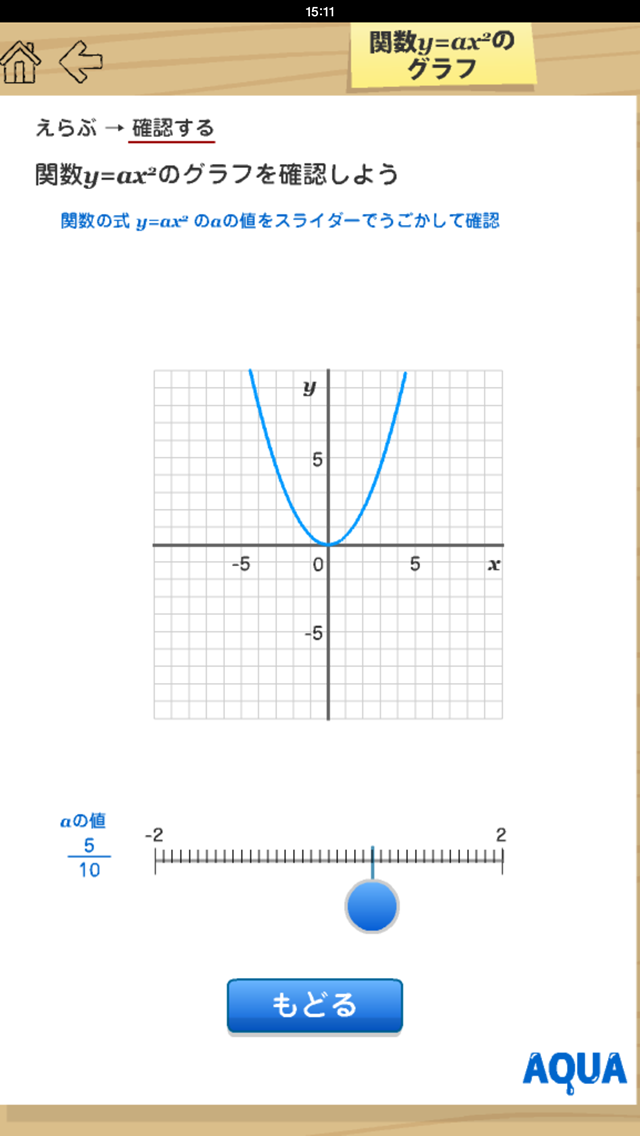
関数y Ax2のグラフ さわってうごく数学 Aquaアクア Iphoneアプリ Applion

二次関数 Wikipedia

高校数学 Y Ax 2のグラフ 下に凸 上に凸 映像授業のtry It トライイット

関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ

2乗に比例する関数のグラフ 放物線 の書き方 無料で使える中学学習プリント

関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ
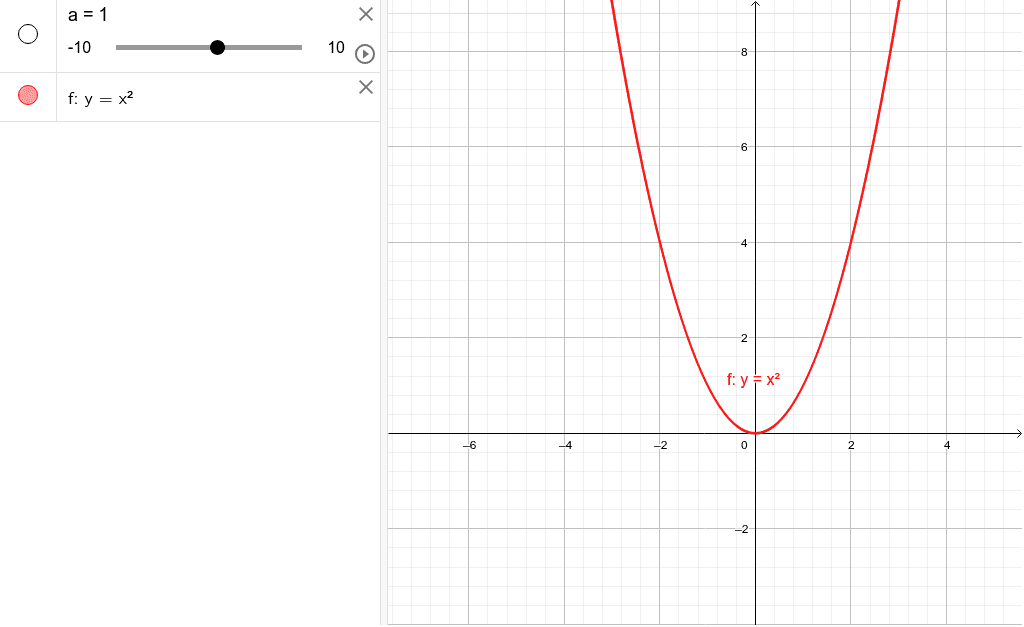
Y Ax 2のグラフ Geogebra
中学数学 関数
グラフを利用して高次不等式を簡単に解く方法 わかるようになる高校数学

二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ

Q Tbn 3aand9gcr3u7a3jgkomdi6kdfbd7atd95s1xtjfc1beg Usqp Cau

Y Ax2乗 Aの求め方についてパターン別に解説 発展問題もアリ 中学数学 理科の学習まとめサイト
数学 二次関数が簡単になる解き方とグラフの書き方 札幌市 学習塾 受験 チーム個別指導塾 大成会
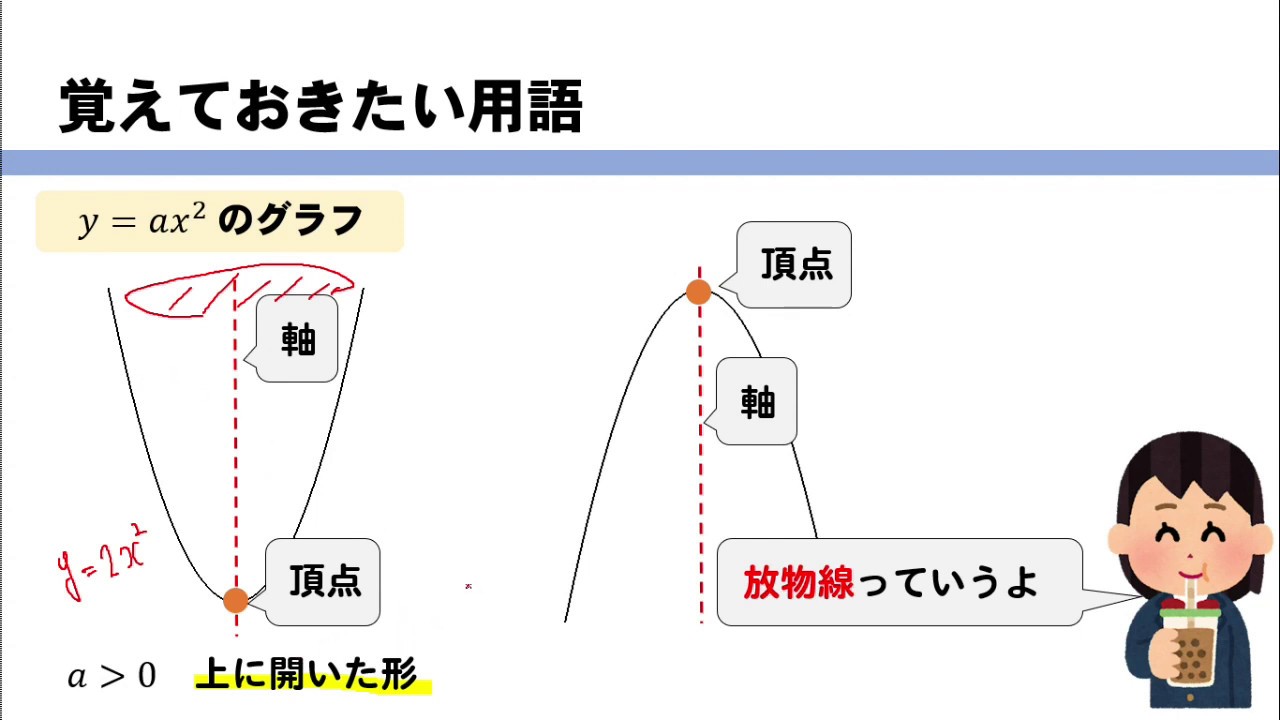
関数y Ax2乗 放物線グラフの書き方はこれでバッチリ Youtube

微分とは何か 中学生でも分かる微分のイメージ

Y Ax 2のグラフ 数学i フリー教材開発コミュニティ Ftext
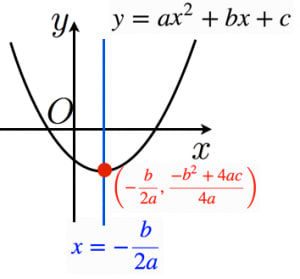
二次関数の軸と頂点の求め方など 高校数学の美しい物語
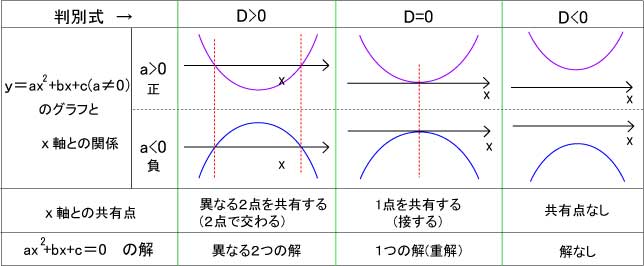
条件より2次関数の方程式を求める

例題で学ぶ高校数学 Y Ax2 Q
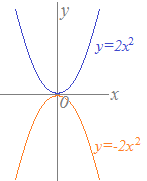
数1 2次関数の用語

中学校数学 3年生 数量 2乗に比例する関数 Wikibooks

関数y Ax2乗の変域の求め方 勉強ナビゲーター

関数 Y Ax2 まとめ 中学生 数学のノート Clear

Y Ax Bのグラフと 切片と傾きの意味 中学数学 By じょばんに マナペディア
2

美園未来塾 高校入試 数学 関数

2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ
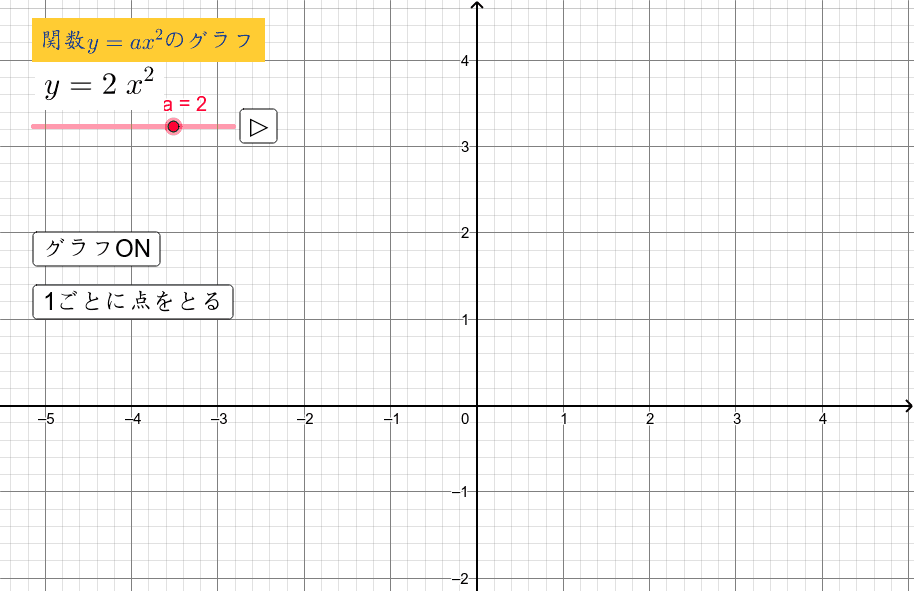
関数y Ax 2のグラフ Geogebra
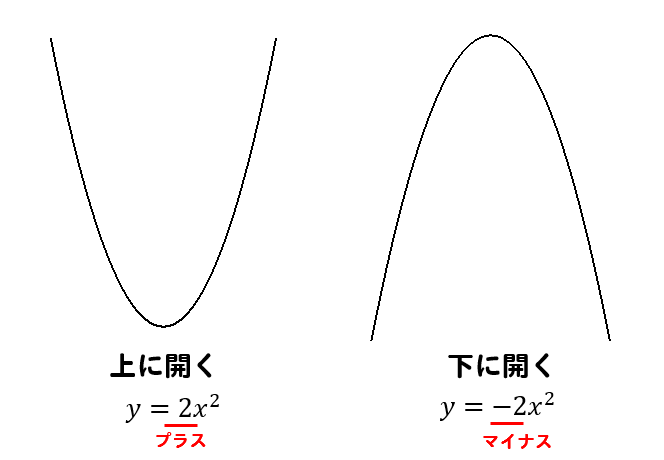
関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ

基礎数学 3回目

2乗に比例する関数のグラフ 放物線 の書き方 無料で使える中学学習プリント
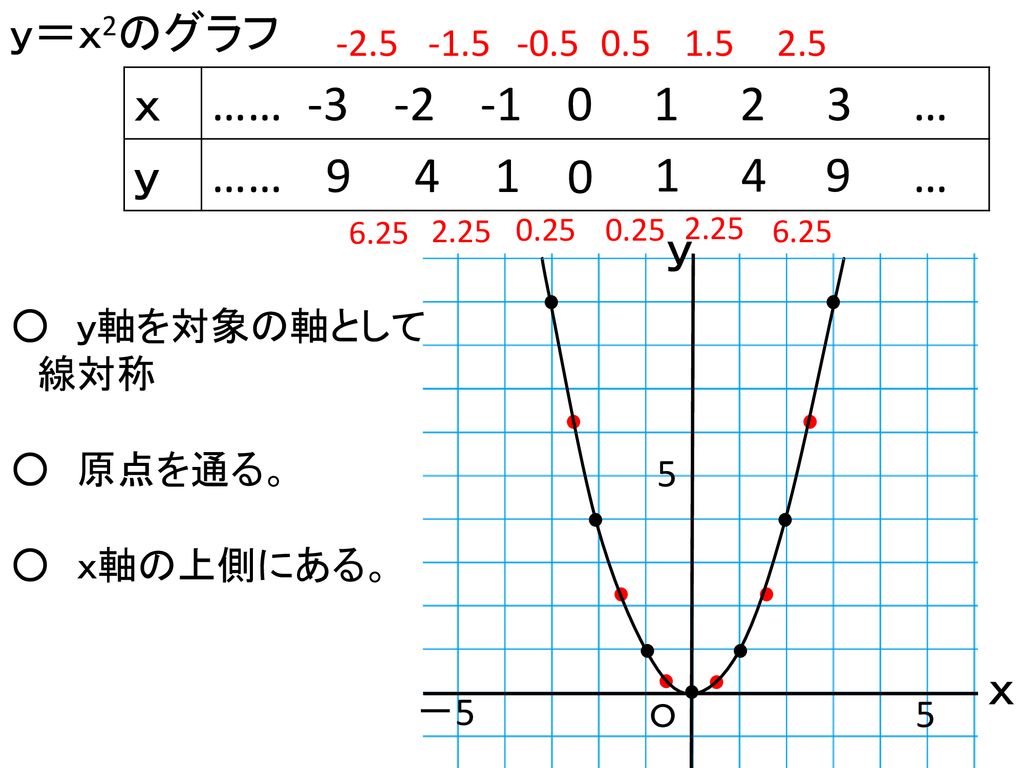
ねらい 関数y ax2のグラフをかき その特徴を理解する Ppt Download
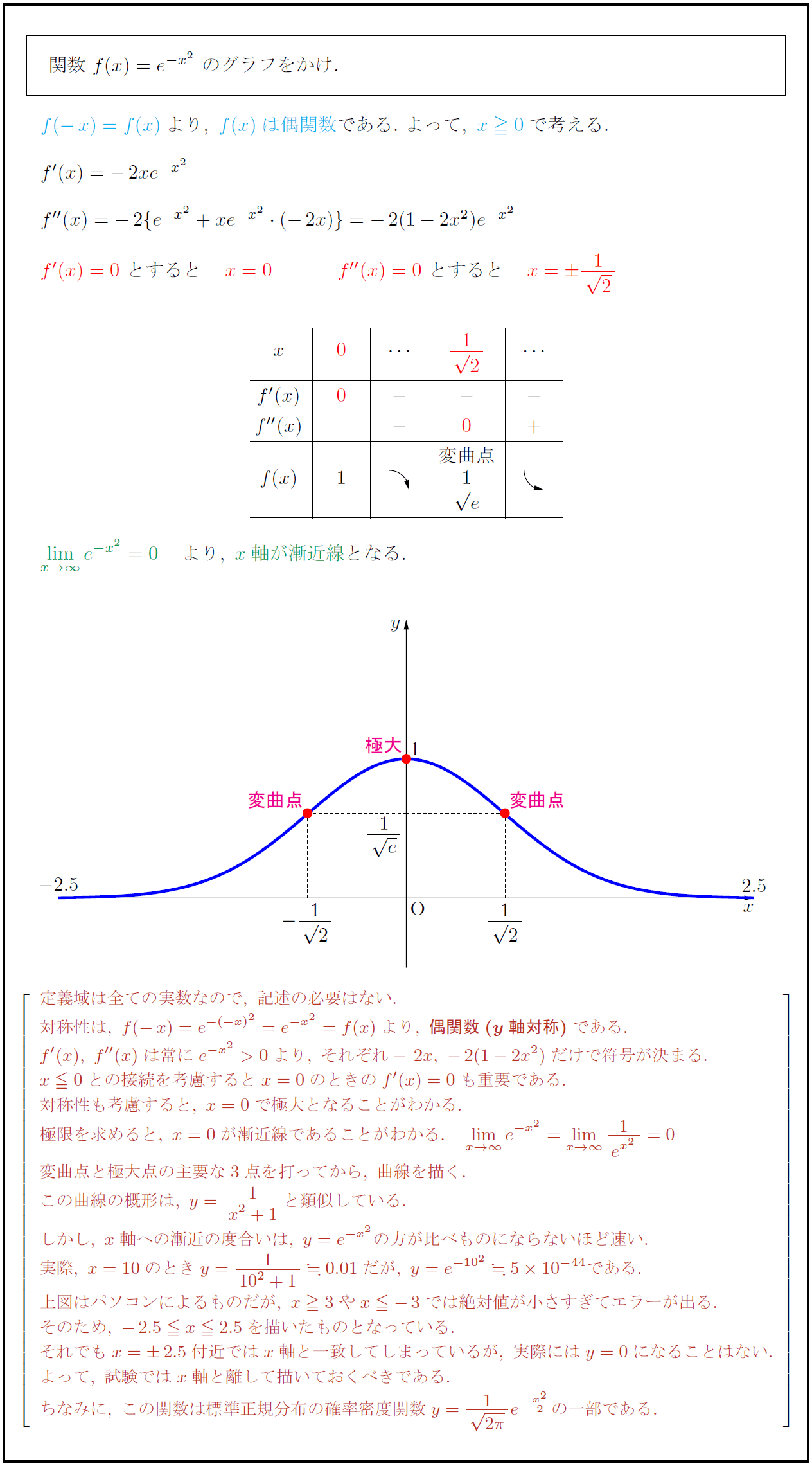
高校数学 指数関数 Y E X のグラフ 正規分布曲線もどき 受験の月
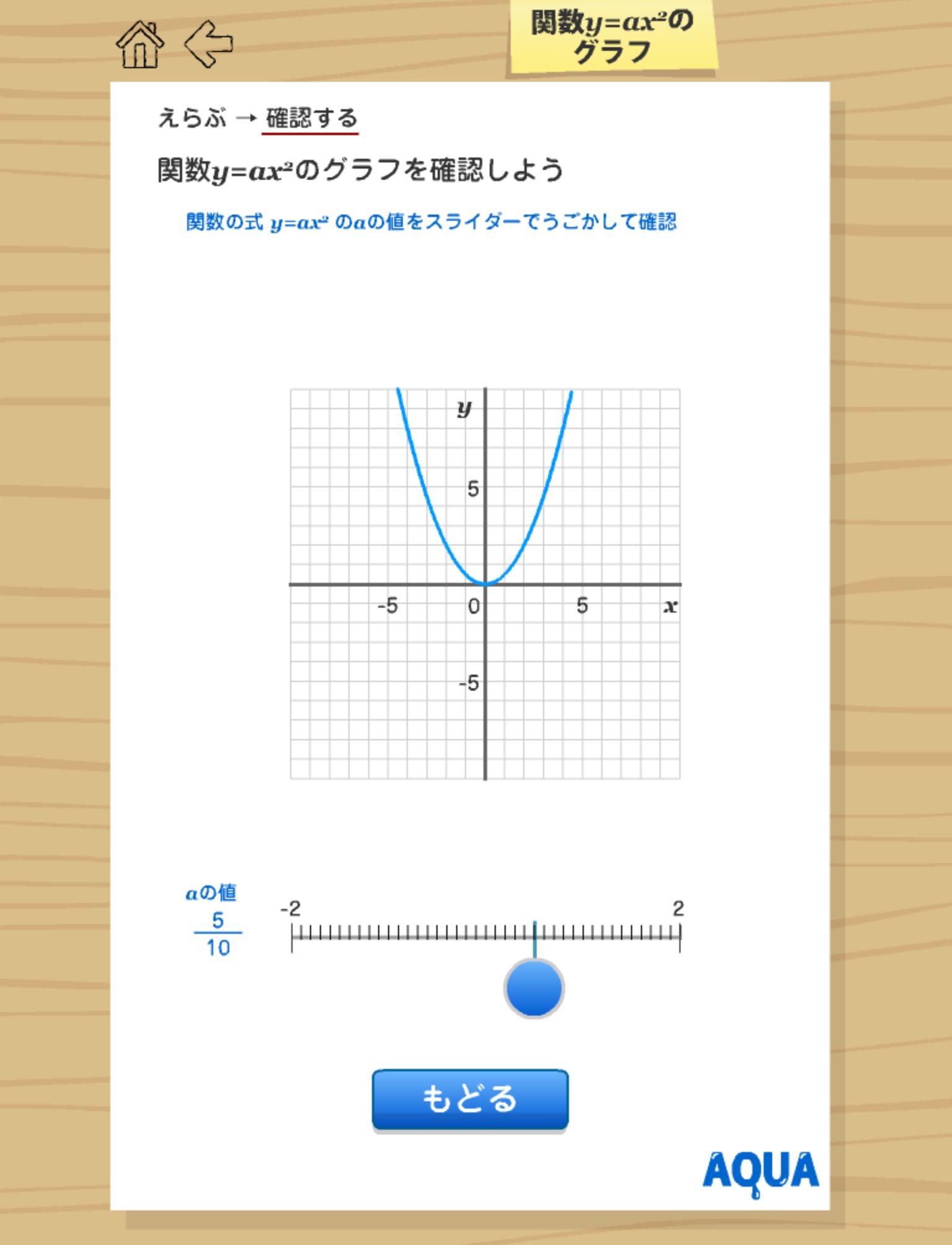
関数y Ax2のグラフ さわってうごく数学 Aquaアクア For Android Apk Download

高校数学 Y Ax 2 Bx Cのグラフ 例題編 映像授業のtry It トライイット
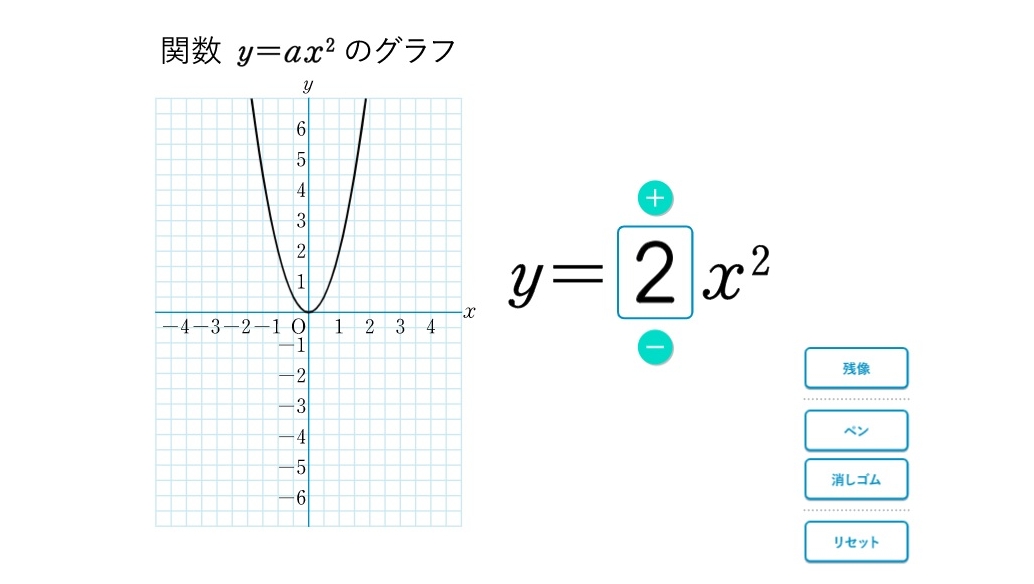
関数y Ax2のグラフ まなびの学園
中学数学 3年 教育出版
二次関数のグラフの書き方
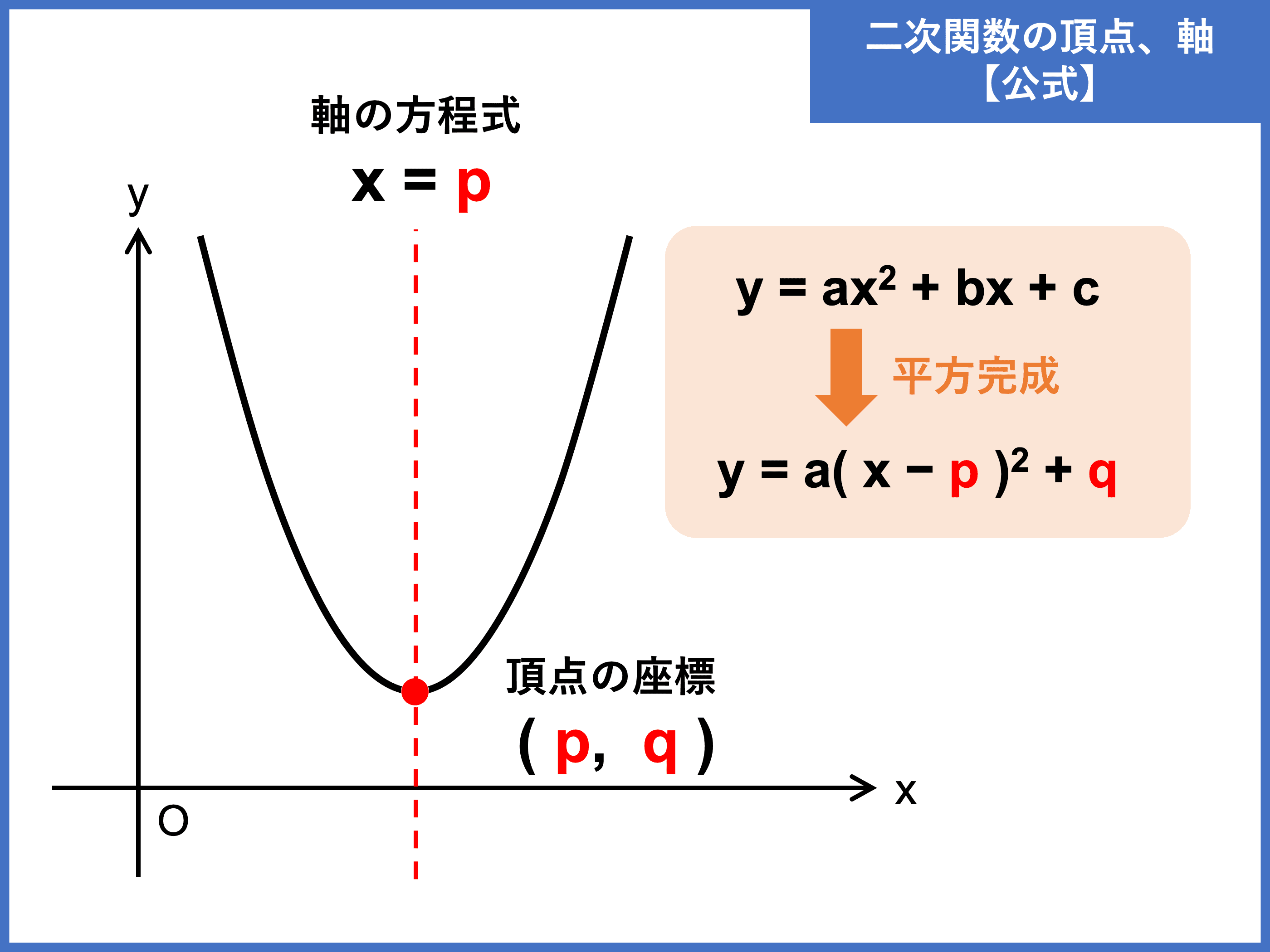
二次関数のグラフの書き方と 頂点 軸 切片の求め方 受験辞典
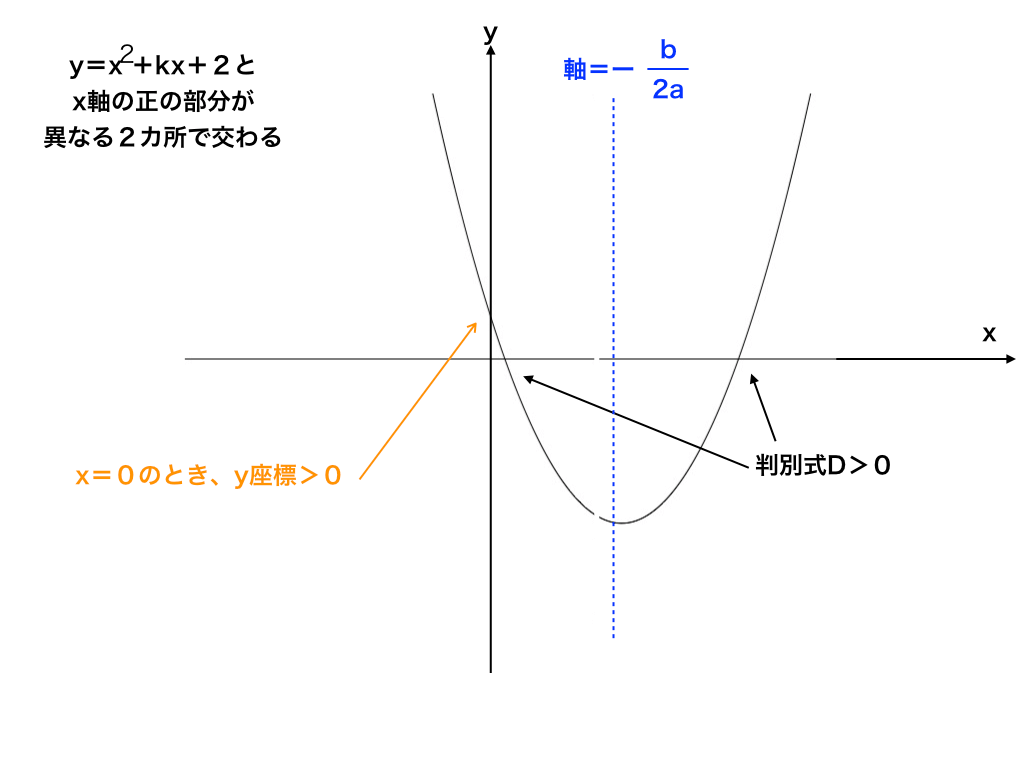
二次関数のグラフと解の存在範囲の問題をわかりやすく解説

基本 二次関数 Y Ax 2 のグラフ なかけんの数学ノート
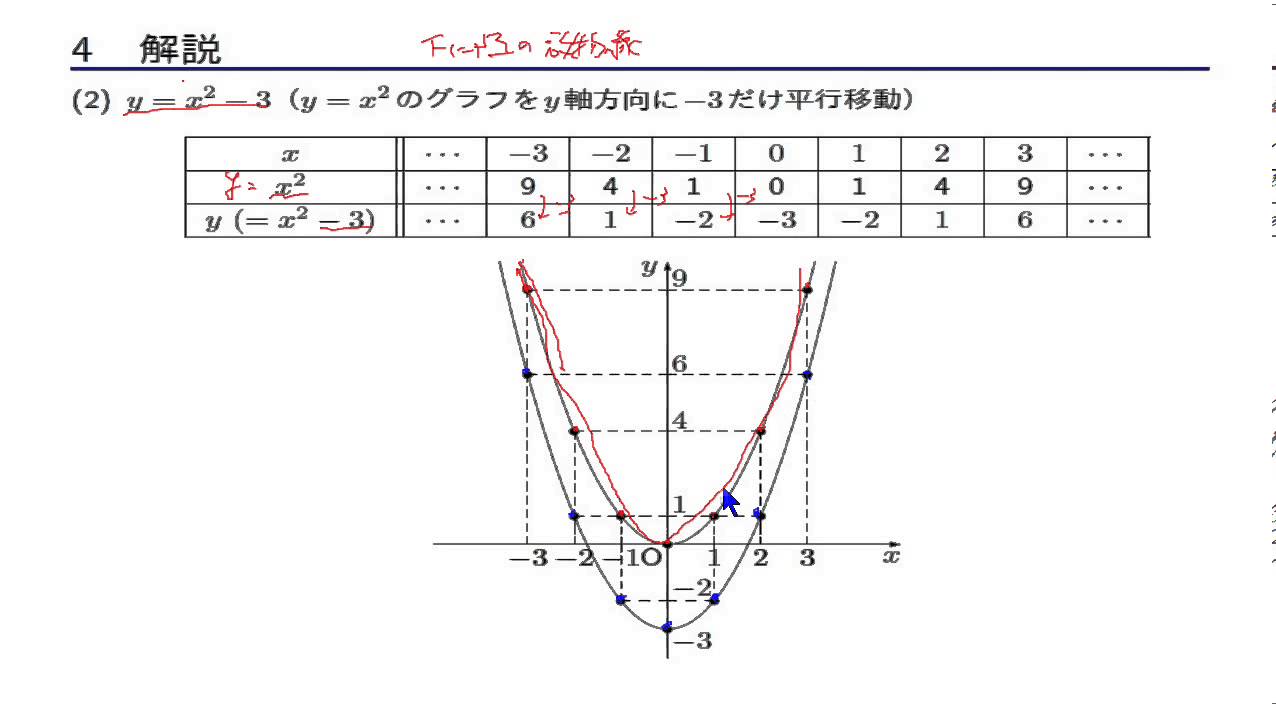
数学i 2次関数 2 2 Y Ax 2 Qのグラフ Youtube
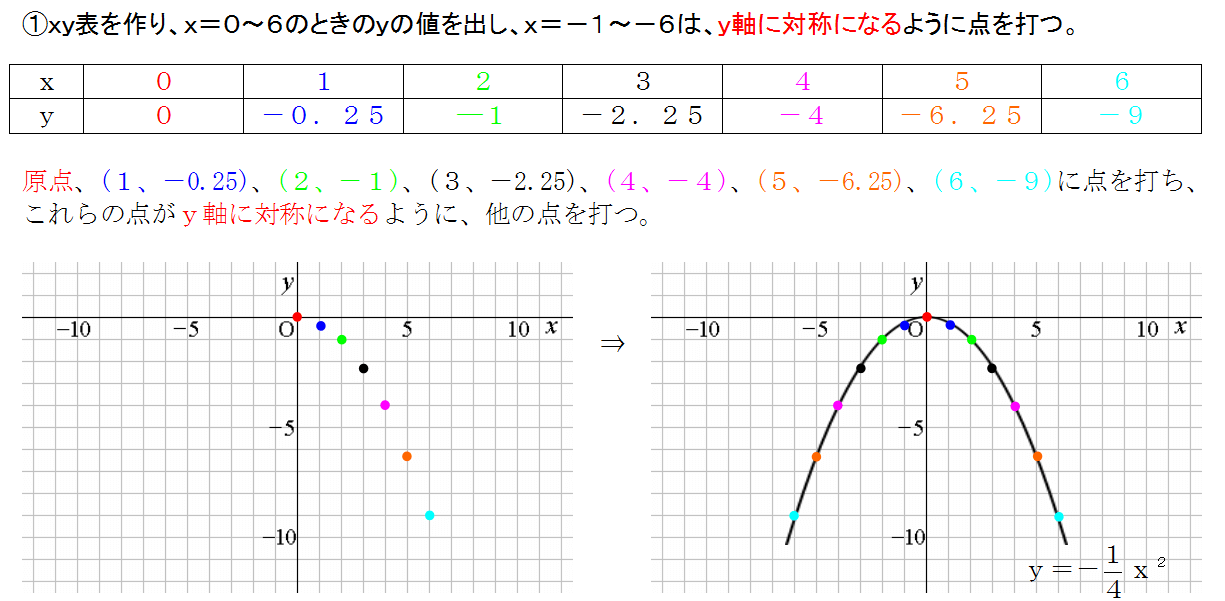
二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師
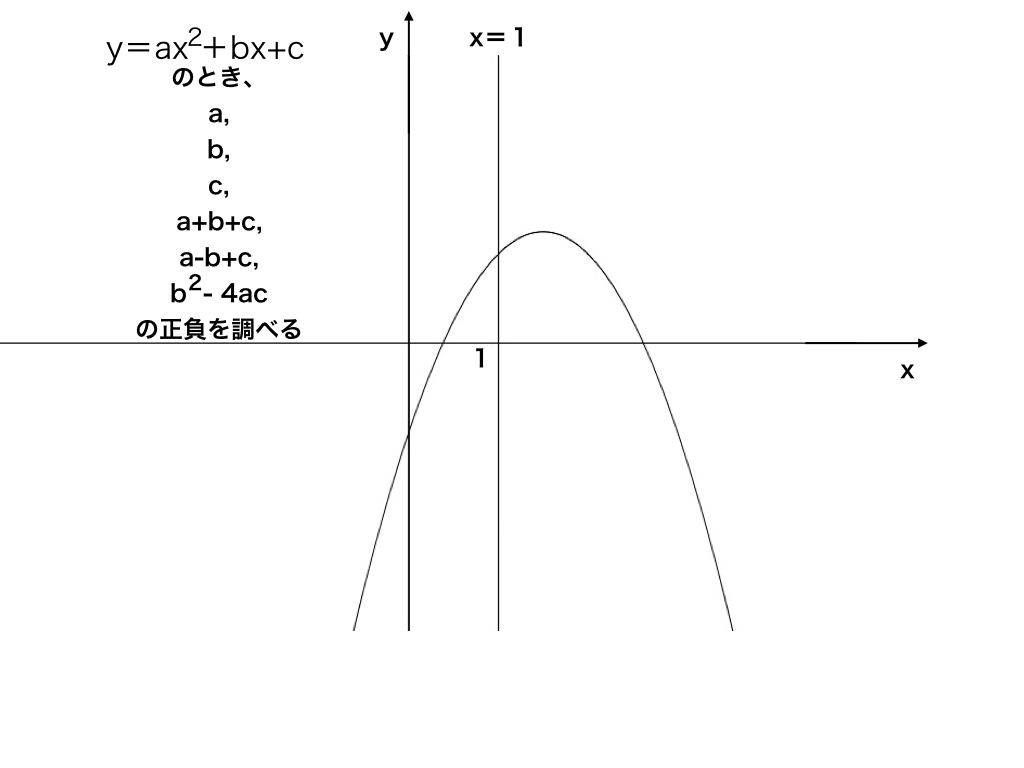
二次関数のグラフと解の存在範囲の問題をわかりやすく解説
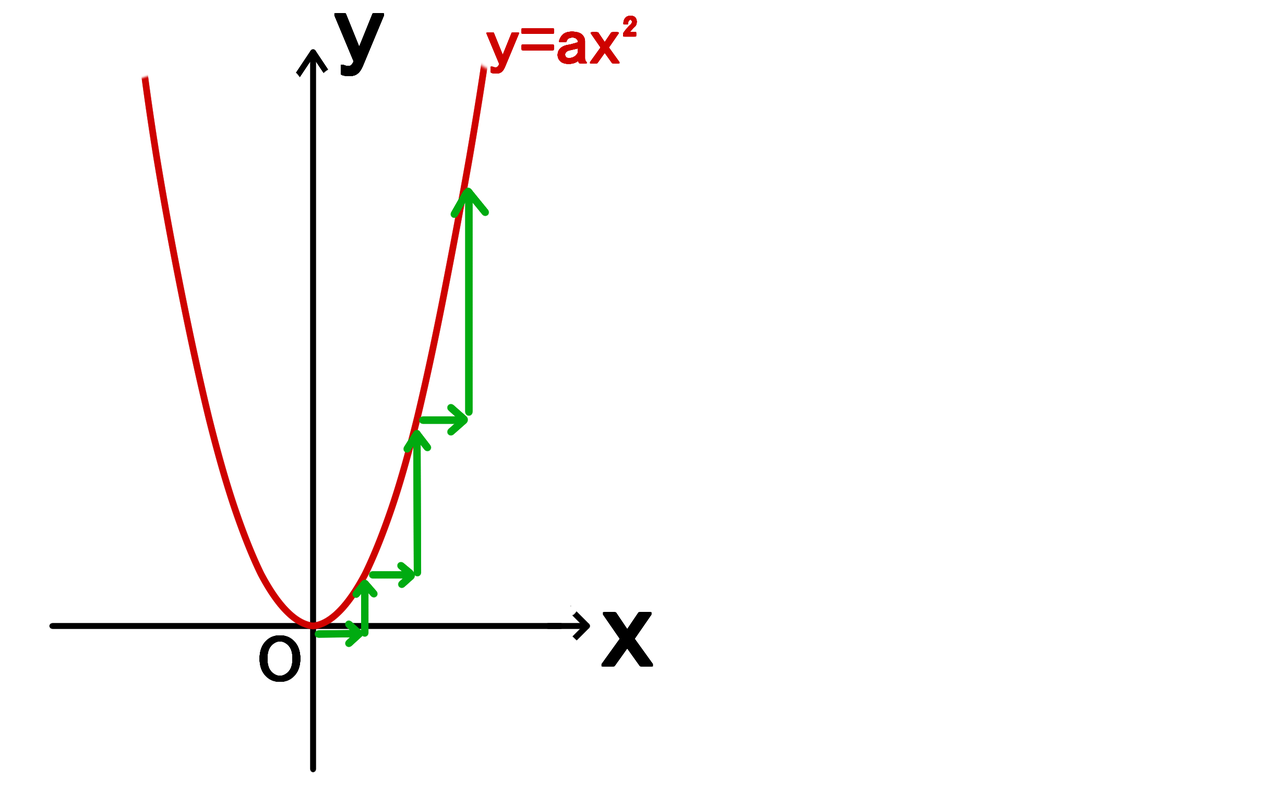
関数y Ax の 変化の割合 の問題 Xの値がaからa 2まで増加したときに Yの値は バカでもわかる 中学数学
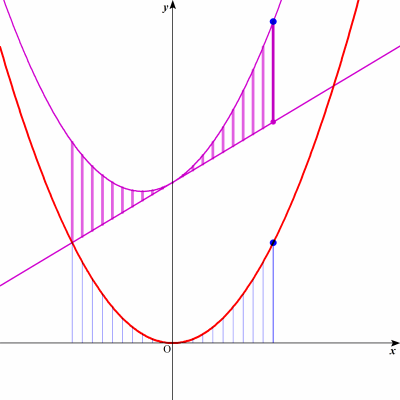
08年9月号の補足

例題で学ぶ高校数学 Y Ax2
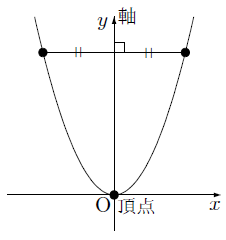
関数y Ax2のグラフ まなびの学園
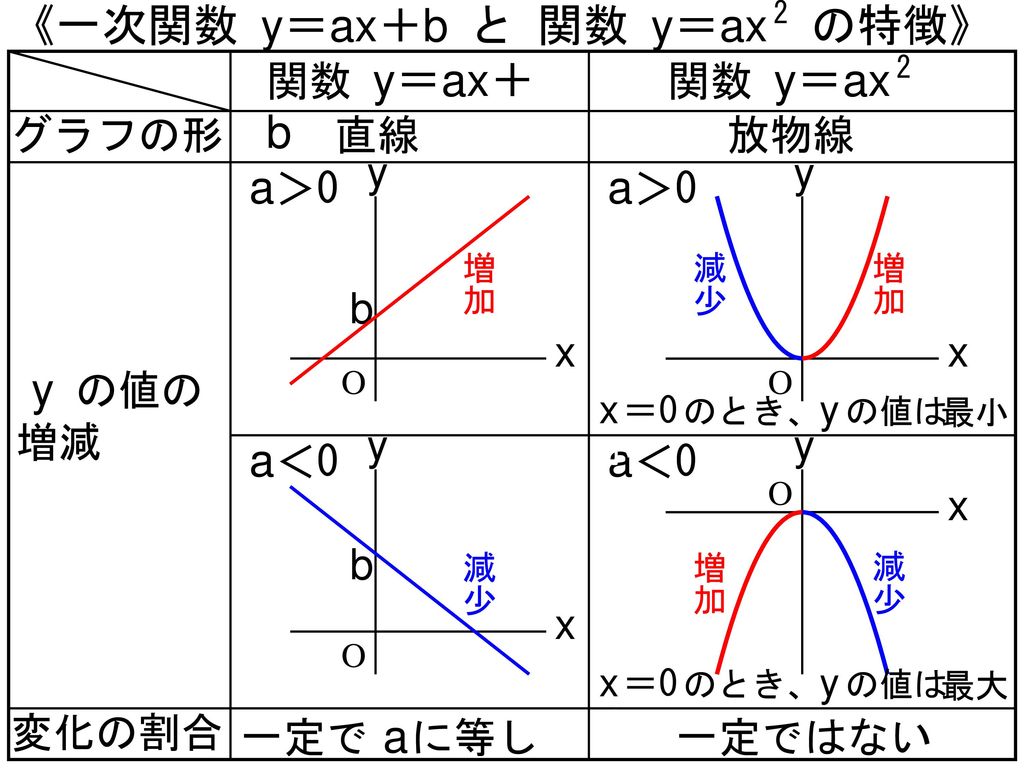
4 関数 Y Ax 2 1章 関数とグラフ 3 関数 Y Ax 2 の値の変化 5時間 Ppt Download
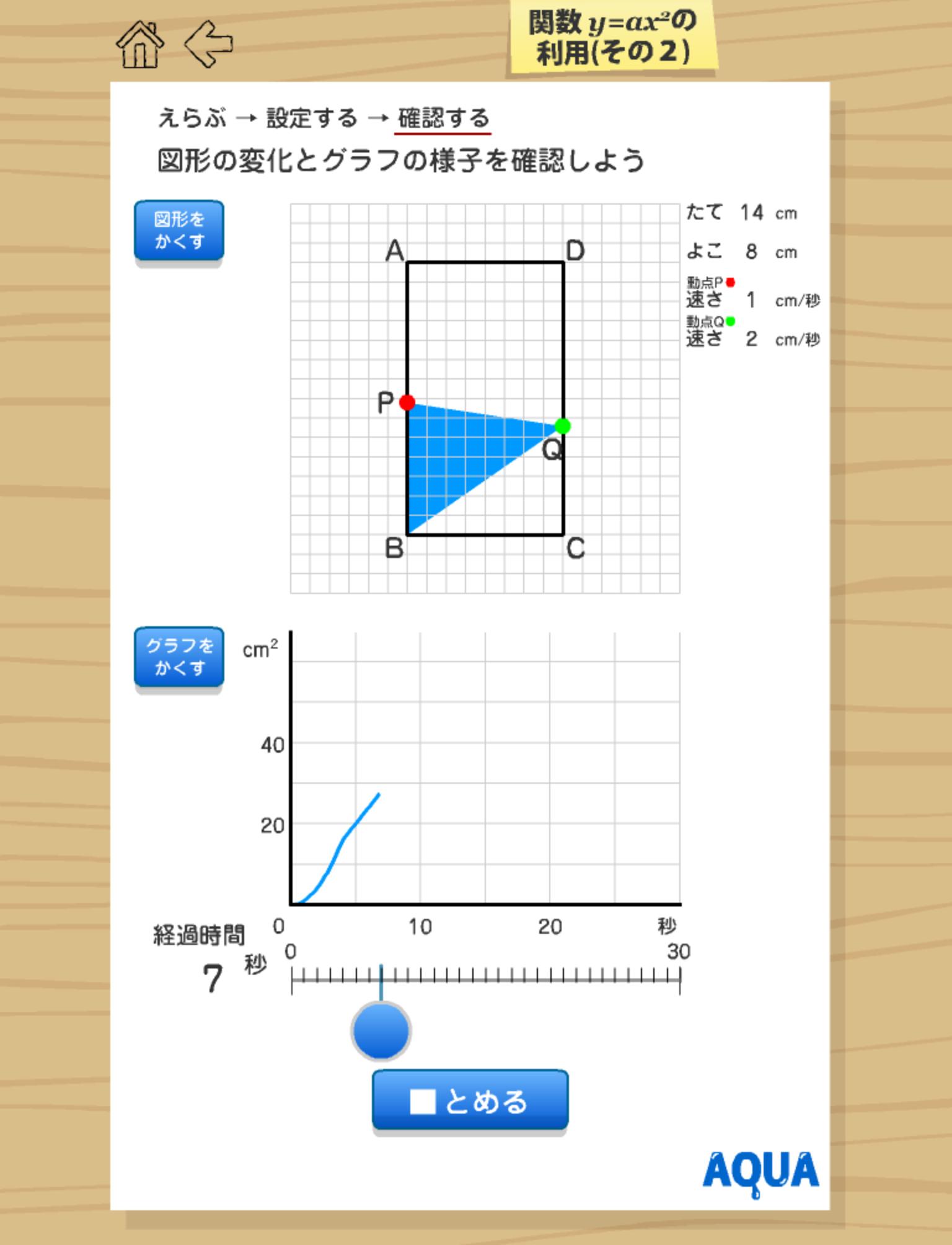
関数y Ax2の利用2 さわってうごく数学 Aquaアクア Fur Android Apk Herunterladen
数学切り抜き帳

関数y Ax2のグラフ まなびの学園




