球 表面積 証明
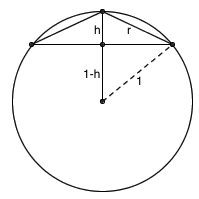
このとき、球冠の表面積の公式 : 球冠の高さを h とすると、側面積 S は、 (ただし、r は、側面の球の半径) (※ 証明はこちら) により、求める表面積Aは、 A=2πr c h により与えられる。.

球 表面積 証明. 球の体積と表面積にについて 1 はじめに 皆さん!どうして半径rの球の体積や表面積が( 4÷3) πr 3 や4πr 2 になるのか不思議に思ったことはありませんか。ここで、一体誰がこのような結果にたどり着くような考え方をしたのかを、今から本を読んで知り得. 球冠,球帯の表面積はその高さに比例する。 注:球帯の高さとは底面と天面の距離です。 球の体積と表面積を積分で証明 の表面積の証明1とほぼ同じことをやるだけです。. 円柱 の にある部分の体積 と表面積 を求めなさい。 練習2.
円の面積の公式や円周率が3より少し大きな数になることの証明である。 聞かれたときにすぐ答え、大人の威厳を取り戻そう。 円を扇形に切って. 3) 円柱面x2 + y2 = a2 の円柱面x2 + z2 = a2 の内部にある部分の曲面積を 求めよ。 4) x-y 平面上のC1 級曲線y = f(x) (a • x • b) をx 軸のまわりに1回転 してできる曲面の曲面積は S = 2… Z b a jf(x)j p 1+(f0(x))2dxとなることを証明せよ。 5) 曲面z = Arctan(y=x) (x;y > 0) の円柱面x2 +y2 = a2 の内部にある部 分の曲面積を. 球の体積と表面積について 新潟県立阿賀黎明高等学校 西條和久 平成14年11月29日 1 はじめに 来年度より,新学習指導要領が実施され,いくつかの中学校の内容が高校へ移行する。.
数学・算数 - 赤血球の表面積を算出する公式について 大学の授業で出された課題についてです。 赤血球がくぼんでいるのは表面積を大きくするためですが、本当に大きくなっているのか証明しなさいと言われ、同じ. Περὶ σφαίρας καὶ κυλίνδρου )は、紀元前225年ごろアルキメデスにより発表された2巻からなる著作 。 最も注目すべきは、球面の表面積や球体の体積、円柱のそれにあたる値を見つけ出す方法が詳しく書かれていることであり、アルキメデスはこれ. 球の表面積の公式はおぼえられた?? 9匹(球)のヒョウ(表面積)の捕獲に失敗(4π)したあるじ(rの二乗) という語呂さえおぼえておけ.
球の表面積と体積を求める公式を紹介します。 シンプルに 球の表面積 球の体積 の2種類の公式だけです。とても重要なのでしっかり覚えておきましょう。. 球の表面積を求める公式は、S = 4πr^2 で表されます。このページでは、例題と共に、この公式の使い方を説明しています。. この記事では、「球」についての公式(体積・表面積)や実際の求め方をできるだけわかりやすく解説していきます。 また、なぜ公式が成り立つかも証明していきます。この記事を通してぜひマスターしてくださいね。 目次球とは?球の.
「球の体積」については覚えなくていい「円の面積」 - 算数は得意なのに数学が苦手なひとのためのブログを見てみてください。 mynkit 19:12 覚えなくていい「球の表面積・体積」. 球の表面積は,半径,y,の円に微小な厚みをかけた円帯を足し合わせていったものですから,半球の表面積は, となります. ここで,なぜ,x軸に沿っての積分,dx,ではないか,の説明は, こちら ,のサイトに丁寧に書かれているので,参考にしてみて. 球の表面積 球の表面積=4πr^2 という公式がありますが、なぜそうなるのですか? 中学生にもわかる、説明はあるでしょうか? 私は中学のとき、なぜそうなるのか理由を教えてもらえず、強制的に公式を覚え.
ここで, r, θ, φ の動く範囲は0 ≤ r < ∞, 0 ≤ θ ≤ π, 0 ≤ φ < 2π であ る. 球 の にある部分の体積 と表面積 を求めなさい。 4.練習問題の答え 解答1. 球の表面積と体積 ここでは、球の表面積と体積を求める公式を紹介しましょう。 表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半.
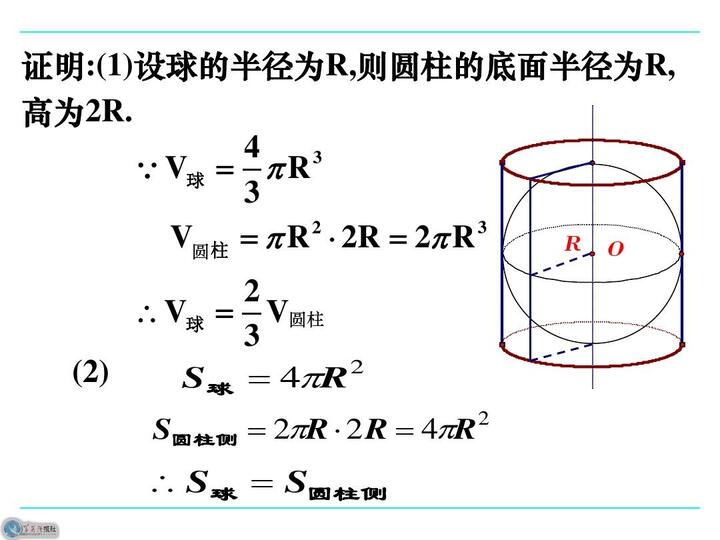
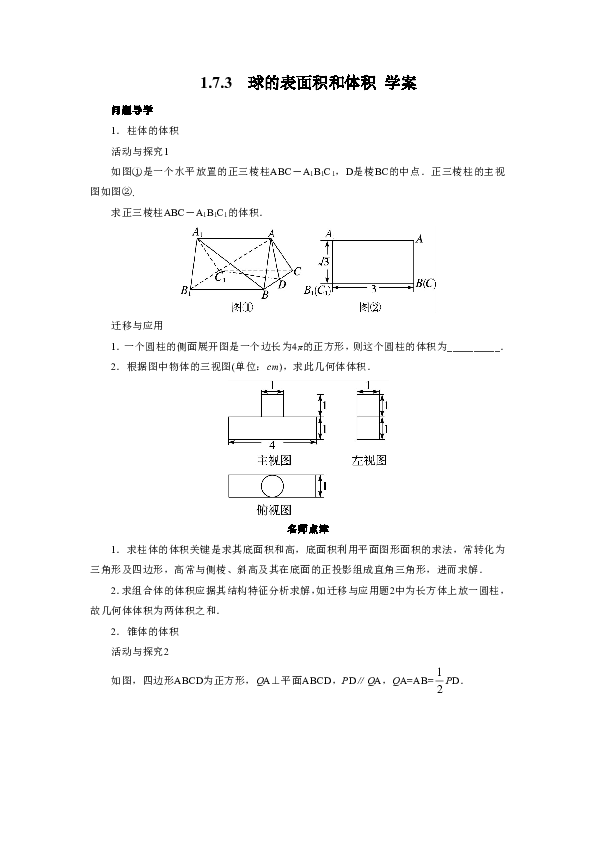
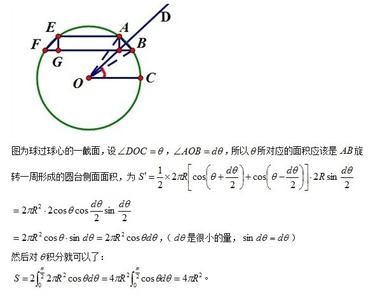
球の表面積の公式、S=4πr 2 とは違ってしまう。 これは、円周の長さを x 方向に積分 するときに、xを微小増加させたときの表面積の変化量が x=0 付近と x=r 付近で異なり、x=r 付近の方が表面積の増加量が大きいためと考えられる。. この証明は球の表面積を積分によって直接求める方法です。 図のような角度が$\theta$から$\theta + \Delta \theta$の青い部分の表面積を考える。 この図形を上から見ると円形になっている。. 球の体積と表面積の公式: 半径 r の球の表面積は S = 4 π r 2, 球の体積は V = 4 3 π r 3 である。.
球の体積と表面積 半径 \\(r\\) の球の体積と表面積を求める公式は以下のようになります。 \\(球の体積=\\displaystyle \\frac{4}{3}\\pi r^3\\) \\(球の表面積=4\\pi r^2\\) 「なぜこの公式が成立するのか」については中学生の知識の範囲外です。 証明には高校数学の「積分」という知識が必要です。 どうし. 球の表面積は、球の半径がrのとき \(4πr^2\) となります。 こちらも球の体積同様に証明の難易度が高く、覚える必要がないため証明は省略します。 公式だけを語呂合わせで覚えてしまいましょう。 球の表面積の公式の覚え方・語呂合わせ. 球の体積の公式を説明していたのを見たような気がする。 このページでは、円や球という図形に的を絞って、その面積や体積・表面積の公式を、直 感的に求める方法について整理しておきたい。 出発点は、まず円周率である。.
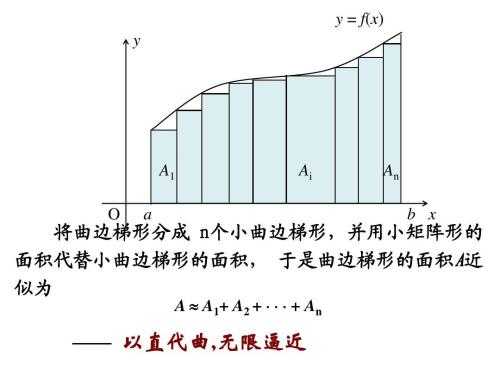
となり、 球の表面積と体積は微分積分の関係にある ことが理解できます。 もちろん(27)式の\(r\)以外の積分を先にやってしまっても同じ結果が出てきます。. 高校数学 kanrinin. この動画を見れば分かります。 「 球の表面積が円の面積の4倍であることの証明 」.
解析学IB・IIA 講義資料 球座標におけるベクトル解析 §1 線素ベクトル・面素ベクトル・体積要素 線素ベクトル 球座標では図1 に示すようにr, θ, φ の値を1 組与えることによって空間の点(r,θ,φ) を指定する. まずは公式を書いておきます。 半径を \(r\) として \(V=\displaystyle\frac{4}{3}\pi r^3\) 証明. 球の表面積の場合は、 球面の全てを覆うように積分範囲を指定する必要があったが、 弓形領域の半分の領域 弓形領域の半分の領域 (黄色) の面積を求める場合は $\phi$ に関する積分範囲を $\alpha$ にすると、その領域が覆われる。.

怎么用微积分证明球的表面积和体积公式 你搜我答

球冠表面积推导图解 第1页 一起扣扣网

半圆球体积怎么计算 学习岛
球 表面積 証明 のギャラリー

1 3 2球的体积和表面积 图文 百度文库

球冠表面积推导图解 第1页 要无忧健康图库

阿基米德的神光 球体积和表面积计算公式的数学解释

阿基米德的神光 球体积和表面积计算公式的数学解释
阿基米德求球表面积的方法 数学教学研究 微信公众号文章阅读 Wemp

对球体表面积的证明有什么问题 结果是p 178 R 178 设球半径为r 表面积为s S就相当于对球 上圆的周长一般式积分 S 2 0 R 2p根号下 R 178 X 178 Dx 4p 0 R 根号下 R 178 X 178 P 作业 慧海网

云墨 如何暴力证明球体与圆锥体积公式 哔哩哔哩 つロ干杯 Bilibili
悟空问答 等周图形 为何圆的面积最大 4个回答

球体面积公式是什么 球的面积公式是什么 球体的体积公式是什么 球体积公式是什么

高中数学必修2 证明三棱锥线面垂直 求外接球表面积 爱言情

阿基米德的神光 球体积和表面积计算公式的数学解释

球体体积公式 圆柱体体积公式 四棱台体积公式 圆锥体的体积公式 Www Shianwang Com

脑洞大开的微积分

球体体积推导图解 第1页 要无忧健康图库

高中数学第一章空间几何体1 3空间几何体的表面积与体积2球的体积和表面积教案 新人教a版必修2 Doc 课件巴巴kejian Com

第3讲球的表面积与体积 爱言情

球的表面积和体积 图文 百度文库

证明球表面积的九种方法 Cartesian Coordinates Mathematics Coordinates

高中数学重难点归纳 立体几何中的计算题型一 空间几何体的表面积与体积题型二 多面体与球的切接问题如需资料 请私信留言 高中数学 雪花新闻

官方双语 为什么球的表面积是同样半径圆的面积的四倍 哔哩哔哩 つロ干杯 Bilibili
切片引理和两个意想不到的应用 Matrix67 The Aha Moments

球的表面积公式 球的表面积公式画法

如何用微积分知识推导球的体积公式 作业 慧海网

高中数学第一章空间几何体1 3空间几何体的表面积与体积2球的体积和表面积教案 新人教a版必修2 Doc 课件巴巴kejian Com
球的体积公式 球的体积公式画法

简单的数学 初中生也能推导球的体积公式 叫我笑笑 哔哩哔哩 つロ干杯 Bilibili
球的表面积公式是什么 上幼儿园的小张老师为大家证明

如何不用微积分算个球 网易订阅

球的表面积计算公式 爱言情 爱生活爱言情

球体表面积体积公式 球的面积 球的面积公式 球的面积体积

高中数学重难点归纳 立体几何中的计算题型一 空间几何体的表面积与体积题型二 多面体与球的切接问题如需资料 请私信留言 高中数学 雪花新闻

用微积分解答半径为a的球的表面积 作业 慧海网

球体积公式的求法 图文 百度文库

圆球表面积 球体表面积的公式证明 篆体字转换器

球体公式 球公式 球体体积公式 球体计算公式

阿基米德的神光 球体积和表面积计算公式的数学解释

圆台表面积与体积公式 学习岛

球的表面积公式是什么 上幼儿园的小张老师为大家证明 爱言情

球体表面积体积公式 球的面积 球的面积公式 球的面积体积
球的表面积 腾讯视频
球的表面积公式 腾讯视频

对新编高中数学教材中球面积 球体积公式处理方案的考虑

为什么对球的体积公式进行求导会得到球的表面积公式 知乎

用感覺理解球體表面積公式 Youtube

球体体积公式 第1页 一起扣扣网

圆球表面积 球体表面积的公式证明 篆体字转换器

证明球表面积的九种方法 Mathematics Word Search Puzzle Words
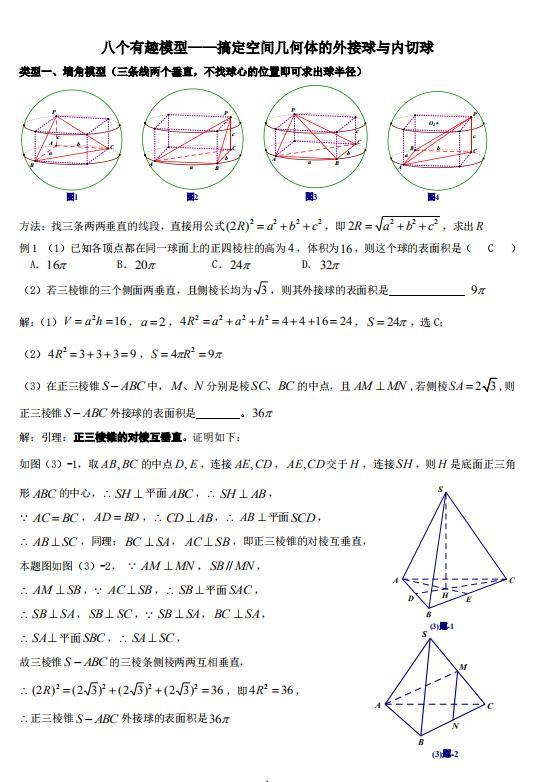
高考数学 八个有趣模型搞定空间几何体的外接球和内切球

脑洞大开的微积分

证明球表面积的九种方法 Mathematics Bullet Journal Surface

求面积公式 相关词 零豆网
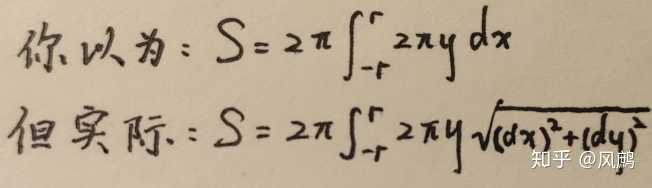
为何对圆周长公式积分无法得到球表面积公式 知乎

重积分法证明球的体积 第1页 一起扣扣网

如何学好高中数学 立体几何之正四面体的内切球和外接球 公式

球的体积公式推导图文 第1页 要无忧健康图库
球的表面积公式 腾讯视频
为什么对球的体积公式进行求导会得到球的表面积公式 知乎

数理天地

空间几何体的表面积和体积讲解及经典例题 上 知识点

重积分法证明球的体积 第1页 一起扣扣网
球的表面积和体积公式推导 手机壁纸 电脑壁纸 桌面壁纸 图客网

530 高中数学空间几何体的表面积和体积
球的表面积和体积 腾讯视频
球的表面积公式 腾讯视频
球体表面积 公式证明 头条百科

呆哥数学二级结论第4课 内接球通用结论 知乎

球体表面积体积公式 球的面积 球的面积公式 球的面积体积
阿基米德的神光 球体积和表面积计算公式的数学解释 看点快报
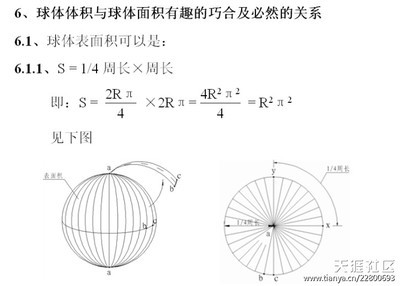
球体的体积公式 圆柱体体积公式 四棱台体积公式 圆锥体的体积公式 Www Shianwang Com

球体积积分公式 球的体积积分 球表面积积分 积分求球体积

高中数学必修2 证明三棱锥线面垂直 求外接球表面积 爱言情
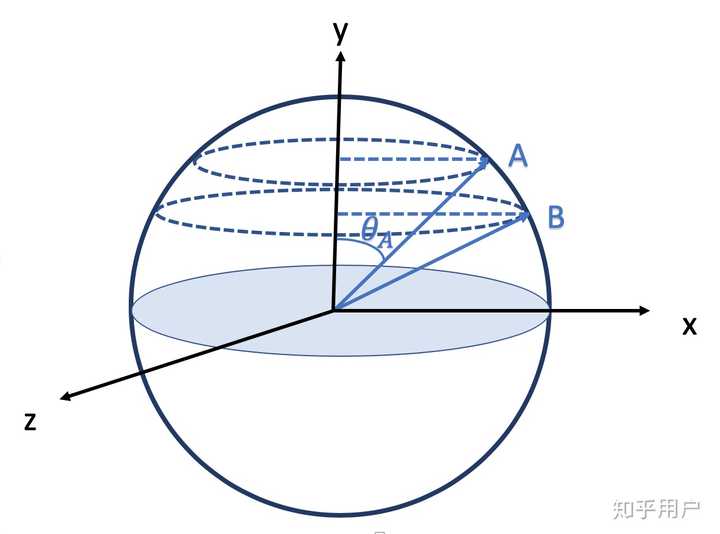
为何对圆周长公式积分无法得到球表面积公式 知乎

球的表面积公式 球的表面积公式画法

如何论证球体体积为4 3pr 3 知乎
球的体积公式 球的体积公式画法

求面积公式 相关词 零豆网

球与球体图形 第1页 一起扣扣网

阿基米德的神光 球体积和表面积计算公式的数学解释

圆球表面积公式推导球体的体积公式 表面积公式的推导

重积分法证明球的体积 第1页 一起扣扣网

对球体表面积的证明有什么问题 结果是p 178 R 178 设球半径为r 表面积为s S就相当于对球 上圆的周长一般式积分 S 2 0 R 2p根号下 R 178 X 178 Dx 4p 0 R 根号下 R 178 X 178 P 作业 慧海网

球的表面积公式是什么 上幼儿园的小张老师为大家证明 爱言情

脑洞大开的微积分

破解世界数学难题 正方体棱切球一作图 二证明 三计算 每日头条
球的表面积 球的表面积画法

7钟搞定一个题丨证明立体几何线面垂直 求三棱锥外接球表面积 第56期 思考

球的体积公式 第3页 一起扣扣网

Smjqrojtcp Bqm
球体表面积公式球体表面积球体表面积 公式证明 爱华网

球体表面积体积公式 球的面积 球的面积公式 球的面积体积
球表面积公式是什么 手机壁纸 电脑壁纸 桌面壁纸 图客网

球的表面积公式图片大全 Uc今日头条新闻网

圆球体积公式怎么推导 相关视频 数学一分钟球的体积公式推导证明 爱言情

球体表面积推导图解 第1页 要无忧健康图库
球体表面积 公式证明 头条百科
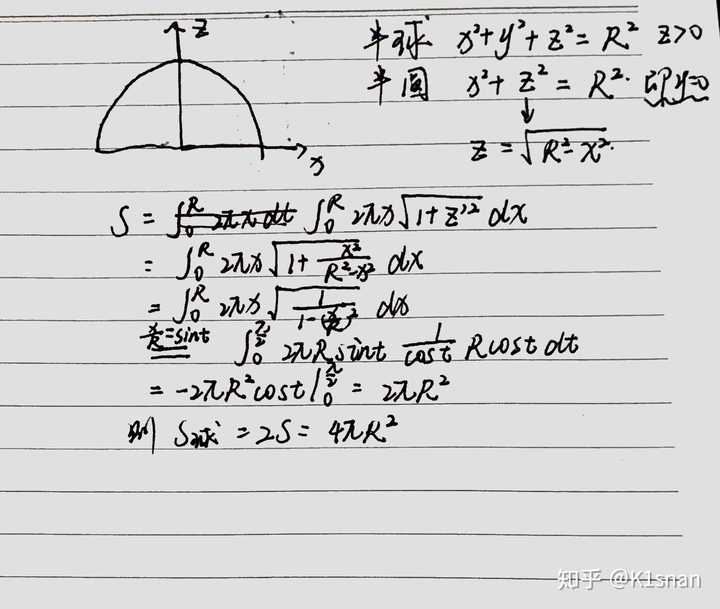
为何对圆周长公式积分无法得到球表面积公式 知乎

勾股定理的证明方法5种 小知识网




